Nomor 1
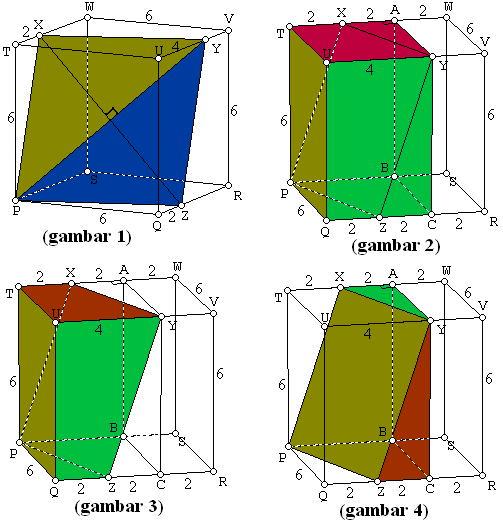
Panjang rusuk kubus PQRS.TUVW adalah 6 cm. Titik X pada TW, Y pada UV, dan Z pada QR. Jika |TX| : |XW| = 1 : 2,
|UY| : |YV| = 2 : 1, dan PXYZ membentuk bidang datar, maka volume bangun TUYX.PQZ adalah ....
$\spadesuit \, $ Gambar

Pada (gambar 1), bidang PXYZ merupakan bidang datar, maksudnya bidang PXYZ merupakan perluasan dari bidang PXY (yang sudah pasti) sehingga memotong rusuk QR di Z. Dengan kata lain, bidang datar yang dimaksud adalah bidang irisan. Untuk menentukan letak titik Z, cukup dengan mencerminkan titik X pada garis PY, sehingga terbentuk garis lurus XZ.
Jika titik Z terletak tidak seperti gambar 1, maka bidang PXYZ yang terbentuk bukan bidang datar lagi melainkan bidang yang melengkung dari bidang PXY ke bidang PYZ yaitu melengkung tepat pada garis PY.
Dengan adanya bidang PXYZ, terbentuklah bangun ruang TUYX.PQZ seperti pada gambar 2.
$\spadesuit \, $ Menentukan volume bangun TUYX.PQZ
Untuk menentukan volume bangun TUYX.PQZ, kita bagi dua bangun tersebut dalam bentuk limas yaitu limas P.TUYX (gambar 3) dan limas P.QZYU (gambar 4) yang masing-masing mempunyai volume yang sama. Sehingga volume bangun TUYX.PQZ adalah dua kali volume salah satu limas.
Limas P.TUYX, alasnya TUYX berupa trapesium dan tinggi trapesiumnya TU, serta tinggi limasnya adalah TP.
$\begin{align} V_{TUYX.PQZ} & = 2 \times V_{\text{limas } P.TUYX} \\ & = 2 \times \frac{1}{3} \times \text{Luas Alas } \times \text{ tinggi} \\ & = 2 \times \frac{1}{3} \times \left[ \frac{1}{2}.(TX + YU).TU \right] \times TP \\ & = \frac{2}{3} \times \left[ \frac{1}{2}.(2+4).6 \right] \times 6 \\ & = 72 \end{align}$
jadi, volume bangun TUYX.PQZ adalah 72 cm$^3 . \heartsuit $

Pada (gambar 1), bidang PXYZ merupakan bidang datar, maksudnya bidang PXYZ merupakan perluasan dari bidang PXY (yang sudah pasti) sehingga memotong rusuk QR di Z. Dengan kata lain, bidang datar yang dimaksud adalah bidang irisan. Untuk menentukan letak titik Z, cukup dengan mencerminkan titik X pada garis PY, sehingga terbentuk garis lurus XZ.
Jika titik Z terletak tidak seperti gambar 1, maka bidang PXYZ yang terbentuk bukan bidang datar lagi melainkan bidang yang melengkung dari bidang PXY ke bidang PYZ yaitu melengkung tepat pada garis PY.
Dengan adanya bidang PXYZ, terbentuklah bangun ruang TUYX.PQZ seperti pada gambar 2.
$\spadesuit \, $ Menentukan volume bangun TUYX.PQZ
Untuk menentukan volume bangun TUYX.PQZ, kita bagi dua bangun tersebut dalam bentuk limas yaitu limas P.TUYX (gambar 3) dan limas P.QZYU (gambar 4) yang masing-masing mempunyai volume yang sama. Sehingga volume bangun TUYX.PQZ adalah dua kali volume salah satu limas.
Limas P.TUYX, alasnya TUYX berupa trapesium dan tinggi trapesiumnya TU, serta tinggi limasnya adalah TP.
$\begin{align} V_{TUYX.PQZ} & = 2 \times V_{\text{limas } P.TUYX} \\ & = 2 \times \frac{1}{3} \times \text{Luas Alas } \times \text{ tinggi} \\ & = 2 \times \frac{1}{3} \times \left[ \frac{1}{2}.(TX + YU).TU \right] \times TP \\ & = \frac{2}{3} \times \left[ \frac{1}{2}.(2+4).6 \right] \times 6 \\ & = 72 \end{align}$
jadi, volume bangun TUYX.PQZ adalah 72 cm$^3 . \heartsuit $
Cara II :
$\spadesuit \, $ Gambar
Pada (gambar 1), bidang PXYZ merupakan bidang datar, maksudnya bidang PXYZ merupakan perluasan dari bidang PXY (yang sudah pasti) sehingga memotong rusuk QR di Z. Dengan kata lain, bidang datar yang dimaksud adalah bidang irisan. Untuk menentukan letak titik Z, cukup dengan mencerminkan titik X pada garis PY, sehingga terbentuk garis lurus XZ.
Jika titik Z terletak tidak seperti gambar 1, maka bidang PXYZ yang terbentuk bukan bidang datar lagi melainkan bidang yang melengkung dari bidang PXY ke bidang PYZ yaitu melengkung tepat pada garis PY.
Dengan adanya bidang PXYZ, terbentuklah bangun ruang TUYX.PQZ seperti pada gambar 3.
$\spadesuit \, $ Menentukan volume bangun TUYX.PQZ
Volume bangun TUYX.PQZ (gambar 3) sama dengan volume bangun AYX.PBCZ (gambar 4). Jika kedua bangun tersebut digabung, maka akan terbentuk balok PBCQ.TAYU seperti gambar 2, yang artinya volume bangun TUYX.PQZ adalah separuh dari volume balok PBCQ.TAYU.
$\begin{align} V_{TUYX.PQZ} & = \frac{1}{2} \times V_{\text{balok } PBCQ.TAYU} \\ & = \frac{1}{2} \times p \times l \times t \\ & = \frac{1}{2} \times QC \times BC \times QU \\ & = \frac{1}{2} \times 4 \times 6 \times 6 \\ & = 72 \end{align}$
jadi, volume bangun TUYX.PQZ adalah 72 cm$^3 . \heartsuit $
$\spadesuit \, $ Gambar

Pada (gambar 1), bidang PXYZ merupakan bidang datar, maksudnya bidang PXYZ merupakan perluasan dari bidang PXY (yang sudah pasti) sehingga memotong rusuk QR di Z. Dengan kata lain, bidang datar yang dimaksud adalah bidang irisan. Untuk menentukan letak titik Z, cukup dengan mencerminkan titik X pada garis PY, sehingga terbentuk garis lurus XZ.
Jika titik Z terletak tidak seperti gambar 1, maka bidang PXYZ yang terbentuk bukan bidang datar lagi melainkan bidang yang melengkung dari bidang PXY ke bidang PYZ yaitu melengkung tepat pada garis PY.
Dengan adanya bidang PXYZ, terbentuklah bangun ruang TUYX.PQZ seperti pada gambar 3.
$\spadesuit \, $ Menentukan volume bangun TUYX.PQZ
Volume bangun TUYX.PQZ (gambar 3) sama dengan volume bangun AYX.PBCZ (gambar 4). Jika kedua bangun tersebut digabung, maka akan terbentuk balok PBCQ.TAYU seperti gambar 2, yang artinya volume bangun TUYX.PQZ adalah separuh dari volume balok PBCQ.TAYU.
$\begin{align} V_{TUYX.PQZ} & = \frac{1}{2} \times V_{\text{balok } PBCQ.TAYU} \\ & = \frac{1}{2} \times p \times l \times t \\ & = \frac{1}{2} \times QC \times BC \times QU \\ & = \frac{1}{2} \times 4 \times 6 \times 6 \\ & = 72 \end{align}$
jadi, volume bangun TUYX.PQZ adalah 72 cm$^3 . \heartsuit $
Nomor 2
Diketahui limas beraturan T.ABCD dengan alas berbentuk persegi dan tinggi limas $ 2\sqrt{3} \, $ cm. Jika $ T^\prime \, $ proyeksi T
pada bidang alas dan titik P adalah perpotongan garis berat segitiga TBC, maka panjang sisi alas limas agar $ T^\prime P \, $ tegak lurus
segitiga TBC adalah .....
$\clubsuit \, $ Gambarnya
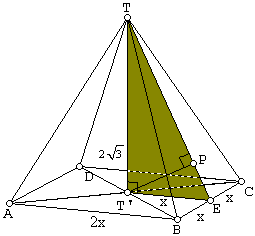
Karena P titik berat, maka panjang $ PE = \frac{1}{3} TE \, $ dan $ PT = \frac{2}{3} TE $
Misalkan panjang $ AB = 2x \, $ sehingga $ BE = EC = T^\prime E = x $
$\clubsuit \, $ Menentukan panjang TE pada segitiga $ TT^\prime E $
$\begin{align} TE & = \sqrt{(TT^\prime )^2 + (T^\prime E)^2 } \\ & = \sqrt{(2\sqrt{3})^2 + x^2 } \\ TE & = \sqrt{12+x^2} \end{align}$
Sehingga panjang :
$ PE = \frac{1}{3} TE = \frac{1}{3} \sqrt{12+x^2} $
$ PT = \frac{2}{3} TE = \frac{2}{3} \sqrt{12+x^2} $
$\clubsuit \, $ Menentukan panjang $ T^\prime P \, $ pada segitiga $ T^\prime PE $
$\begin{align} T^\prime P^2 & = T^\prime E^2 - PE^2 \\ T^\prime P^2 & = x^2 - \left( \frac{1}{3} \sqrt{12+x^2} \right)^2 \\ T^\prime P^2 & = x^2 - \frac{1}{9} (12+x^2) \\ T^\prime P^2 & = \frac{8}{9}x^2 - \frac{4}{3} \end{align}$
$\clubsuit \, $ Menentukan nilai $ x \, $ pada segitiga $ TT^\prime P $
$\begin{align} (TT^\prime )^2 & = T^\prime P^2 + PT^2 \\ (2\sqrt{3})^2 & = \left( \frac{8}{9}x^2 - \frac{4}{3} \right) + \left( \frac{2}{3} \sqrt{12+x^2} \right)^2 \\ 12 & = \frac{8}{9}x^2 - \frac{4}{3} + \frac{4}{9}(12+x^2) \\ 12 & = \frac{8}{9}x^2 - \frac{4}{3} + \frac{16}{3} + \frac{4}{9}x^2 \\ 12 & = \frac{12}{9}x^2 + \frac{12}{3} \\ 12 & = \frac{4}{3}x^2 + 4 \\ x^2 & = 8 . \frac{3}{4} = 6 \\ x & = \sqrt{6} \end{align}$
Sehingga panjang sisi alasnya :
$ AB = 2x = 2\sqrt{6} $
Jadi, panjang sisi alas limas adalah $ 2\sqrt{6}. \heartsuit $
Catatan : Tidak ada pada pilihan (tidak ada jawabannya).

Karena P titik berat, maka panjang $ PE = \frac{1}{3} TE \, $ dan $ PT = \frac{2}{3} TE $
Misalkan panjang $ AB = 2x \, $ sehingga $ BE = EC = T^\prime E = x $
$\clubsuit \, $ Menentukan panjang TE pada segitiga $ TT^\prime E $
$\begin{align} TE & = \sqrt{(TT^\prime )^2 + (T^\prime E)^2 } \\ & = \sqrt{(2\sqrt{3})^2 + x^2 } \\ TE & = \sqrt{12+x^2} \end{align}$
Sehingga panjang :
$ PE = \frac{1}{3} TE = \frac{1}{3} \sqrt{12+x^2} $
$ PT = \frac{2}{3} TE = \frac{2}{3} \sqrt{12+x^2} $
$\clubsuit \, $ Menentukan panjang $ T^\prime P \, $ pada segitiga $ T^\prime PE $
$\begin{align} T^\prime P^2 & = T^\prime E^2 - PE^2 \\ T^\prime P^2 & = x^2 - \left( \frac{1}{3} \sqrt{12+x^2} \right)^2 \\ T^\prime P^2 & = x^2 - \frac{1}{9} (12+x^2) \\ T^\prime P^2 & = \frac{8}{9}x^2 - \frac{4}{3} \end{align}$
$\clubsuit \, $ Menentukan nilai $ x \, $ pada segitiga $ TT^\prime P $
$\begin{align} (TT^\prime )^2 & = T^\prime P^2 + PT^2 \\ (2\sqrt{3})^2 & = \left( \frac{8}{9}x^2 - \frac{4}{3} \right) + \left( \frac{2}{3} \sqrt{12+x^2} \right)^2 \\ 12 & = \frac{8}{9}x^2 - \frac{4}{3} + \frac{4}{9}(12+x^2) \\ 12 & = \frac{8}{9}x^2 - \frac{4}{3} + \frac{16}{3} + \frac{4}{9}x^2 \\ 12 & = \frac{12}{9}x^2 + \frac{12}{3} \\ 12 & = \frac{4}{3}x^2 + 4 \\ x^2 & = 8 . \frac{3}{4} = 6 \\ x & = \sqrt{6} \end{align}$
Sehingga panjang sisi alasnya :
$ AB = 2x = 2\sqrt{6} $
Jadi, panjang sisi alas limas adalah $ 2\sqrt{6}. \heartsuit $
Catatan : Tidak ada pada pilihan (tidak ada jawabannya).
Nomor 3
Titik pusat lingkaran yang menyinggung garis $ y = 2 \, $ di (3,2) dan menyinggung garis $ y = -x\sqrt{3} + 2 \, $ adalah ....
$\spadesuit \, $ Gambar

Ada dua lingkaran yang terbentuk yang menyinggung kedua garis.
Untuk menentukan titik pusat lingkaran, kita menggunakan konsep jarak titik pusat ke garis singgung lingkarannya sama dengan jari-jari lingkaran.
Persamaan garisnya : $ y = -x\sqrt{3} + 2 \, $ atau $ \sqrt{3} x + y - 2 = 0 $
$\spadesuit \, $ Konsep jarak titik ke garis
Jarak titik $(m,n)\, $ ke garis $ ax+by+c=0 \, $
Jarak = $ \left| \frac{a.m+b.n+c}{\sqrt{a^2+b^2}} \right| $
$\spadesuit \, $ Titik pusat lingkaran I (LI) :
Jarak titik pusat $(3,a) \, $ ke garis $ \sqrt{3} x + y - 2 = 0 $
Jarak $ = \left| \frac{a.m+b.n+c}{\sqrt{a^2+b^2}} \right| = \left| \frac{\sqrt{3} .3 + a - 2}{\sqrt{(\sqrt{3})^2+1^2}} \right| = \frac{3\sqrt{3} + a - 2}{2} $
Jari-jari = $ r_1 = 2 - a $
*). Menentukan nilai $ a \, $ :
$ \begin{align} \text{ jari - jari } & = \text{ jarak } \\ \frac{3\sqrt{3} + a - 2}{2} & = 2 - a \\ 3\sqrt{3} + a - 2 & = 2(2-a) \\ 3a & = 6 - 3\sqrt{3} \\ a & = 2 - \sqrt{3} \end{align} $
Sehingga titik pusat lingkaran I : $ (3, a ) = (3, 2-\sqrt{3}) $
$\spadesuit \, $ Titik pusat lingkaran II (LII) :
Jarak titik pusat $(3,b) \, $ ke garis $ \sqrt{3} x + y - 2 = 0 $
Jarak $ = \left| \frac{a.m+b.n+c}{\sqrt{a^2+b^2}} \right| = \left| \frac{\sqrt{3} .3 + b - 2}{\sqrt{(\sqrt{3})^2+1^2}} \right| = \frac{3\sqrt{3} + b - 2}{2} $
Jari-jari = $ r_2 = b - 2 $
*). Menentukan nilai $ b \, $ :
$ \begin{align} \text{ jari - jari } & = \text{ jarak } \\ \frac{3\sqrt{3} + b - 2}{2} & = b - 2 \\ 3\sqrt{3} + b - 2 & = 2(b-2) \\ b & = 2 + 3\sqrt{3} \end{align} $
Sehingga titik pusat lingkaran II : $ (3, b ) = (3, 2+3\sqrt{3}) $
Pada pilihan yang ada adalah lingkaran II.
Jadi, salah satu pusat lingkarannya adalah $ (3, 2+3\sqrt{3}) . \heartsuit $

Ada dua lingkaran yang terbentuk yang menyinggung kedua garis.
Untuk menentukan titik pusat lingkaran, kita menggunakan konsep jarak titik pusat ke garis singgung lingkarannya sama dengan jari-jari lingkaran.
Persamaan garisnya : $ y = -x\sqrt{3} + 2 \, $ atau $ \sqrt{3} x + y - 2 = 0 $
$\spadesuit \, $ Konsep jarak titik ke garis
Jarak titik $(m,n)\, $ ke garis $ ax+by+c=0 \, $
Jarak = $ \left| \frac{a.m+b.n+c}{\sqrt{a^2+b^2}} \right| $
$\spadesuit \, $ Titik pusat lingkaran I (LI) :
Jarak titik pusat $(3,a) \, $ ke garis $ \sqrt{3} x + y - 2 = 0 $
Jarak $ = \left| \frac{a.m+b.n+c}{\sqrt{a^2+b^2}} \right| = \left| \frac{\sqrt{3} .3 + a - 2}{\sqrt{(\sqrt{3})^2+1^2}} \right| = \frac{3\sqrt{3} + a - 2}{2} $
Jari-jari = $ r_1 = 2 - a $
*). Menentukan nilai $ a \, $ :
$ \begin{align} \text{ jari - jari } & = \text{ jarak } \\ \frac{3\sqrt{3} + a - 2}{2} & = 2 - a \\ 3\sqrt{3} + a - 2 & = 2(2-a) \\ 3a & = 6 - 3\sqrt{3} \\ a & = 2 - \sqrt{3} \end{align} $
Sehingga titik pusat lingkaran I : $ (3, a ) = (3, 2-\sqrt{3}) $
$\spadesuit \, $ Titik pusat lingkaran II (LII) :
Jarak titik pusat $(3,b) \, $ ke garis $ \sqrt{3} x + y - 2 = 0 $
Jarak $ = \left| \frac{a.m+b.n+c}{\sqrt{a^2+b^2}} \right| = \left| \frac{\sqrt{3} .3 + b - 2}{\sqrt{(\sqrt{3})^2+1^2}} \right| = \frac{3\sqrt{3} + b - 2}{2} $
Jari-jari = $ r_2 = b - 2 $
*). Menentukan nilai $ b \, $ :
$ \begin{align} \text{ jari - jari } & = \text{ jarak } \\ \frac{3\sqrt{3} + b - 2}{2} & = b - 2 \\ 3\sqrt{3} + b - 2 & = 2(b-2) \\ b & = 2 + 3\sqrt{3} \end{align} $
Sehingga titik pusat lingkaran II : $ (3, b ) = (3, 2+3\sqrt{3}) $
Pada pilihan yang ada adalah lingkaran II.
Jadi, salah satu pusat lingkarannya adalah $ (3, 2+3\sqrt{3}) . \heartsuit $
Nomor 4
Diberikan koordinat titik O(0,0), B($-3,\sqrt{7}$), dan A($a,0$), dengan $ a > 0. \, $ Jika pada segitiga AOB, $ \angle OAB = \alpha \, $
dan $ \angle OBA = \beta, \, $ maka $ \cos \frac{1}{2} (\alpha + \beta ) = .... $
$\spadesuit \, $ Gambar
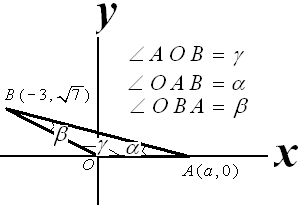
Jarak dua titik $(a,b) \, $ dan $ (m,n) $
Jarak $ = \sqrt{(m-a)^2 + (n-b)^2} $
$\spadesuit \, $ Menentukan panjang masing-masing
$ AB = \sqrt{(a-(-3))^2 + (\sqrt{7} - 0 )^2 } $
$ AB^2 = (a+3)^2 + 7 $
$ OB = \sqrt{(-3-0)^2 + (\sqrt{7}-0)^2 } \rightarrow OB = \sqrt{16} = 4 $
$ OA^2 = a^2 \rightarrow OA = a $
$\spadesuit \, $ Menentukan nilai $ \cos AOB $
$\begin{align} AB^2 & = OA^2 + OB^2 - 2.OA.OB. \cos AOB \\ \cos AOB & = \frac{OA^2 + OB^2 - AB^2}{2.OA.OB} \\ \cos \gamma & = \frac{OA^2 + OB^2 - AB^2}{2.OA.OB} \\ \cos \gamma & = \frac{a^2 + 16 - [(a+3)^2 + 7]}{2.a.4} \\ \cos \gamma & = \frac{a^2 + 16 - [a^2 + 6a + 16]}{2.a.4} \\ \cos \gamma & = \frac{-6a}{2.a.4} = \frac{-3}{4} \end{align}$
$\spadesuit \, $ Menentukan nilai $ \sin \frac{1}{2} \gamma $
Konsep dasar : $ \cos px = 1 - 2 \sin ^2 \frac{1}{2}p x $
Sehingga : $ \cos x = 1 - 2 \sin ^2 \frac{1}{2} x $
$\begin{align} \cos \gamma & = 1 - 2 \sin ^2 \frac{1}{2} \gamma \\ \sin \frac{1}{2} \gamma & = \sqrt{\frac{1}{2} - \frac{1}{2} \cos \gamma } \\ \sin \frac{1}{2} \gamma & = \sqrt{\frac{1}{2} - \frac{1}{2} . ( \frac{-3}{4} ) } \\ \sin \frac{1}{2} \gamma & = \sqrt{\frac{7}{8}} = \sqrt{ \frac{7}{8} . \frac{2}{2}} = \frac{1}{4} \sqrt{14} \end{align}$
$\spadesuit \, $ Menentukan nilai $ \cos \frac{1}{2} ( \alpha + \beta ) \, $ pada segitiga AOB
$\begin{align} \alpha + \beta + \gamma & = 180^\circ \\ \alpha + \beta & = 180^\circ - \gamma \\ \frac{1}{2} (\alpha + \beta ) & = \frac{1}{2} (180^\circ - \gamma ) \\ \frac{1}{2} (\alpha + \beta ) & = 90^\circ - \frac{1}{2} \gamma \\ \cos \frac{1}{2} (\alpha + \beta ) & = \cos ( 90^\circ - \frac{1}{2} \gamma ) \\ & = \sin \frac{1}{2} \gamma \\ & = \frac{1}{4} \sqrt{14} \end{align}$
Jadi, nilai $ \cos \frac{1}{2} (\alpha + \beta ) = \frac{1}{4} \sqrt{14} . \heartsuit $
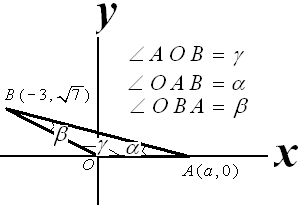
Jarak dua titik $(a,b) \, $ dan $ (m,n) $
Jarak $ = \sqrt{(m-a)^2 + (n-b)^2} $
$\spadesuit \, $ Menentukan panjang masing-masing
$ AB = \sqrt{(a-(-3))^2 + (\sqrt{7} - 0 )^2 } $
$ AB^2 = (a+3)^2 + 7 $
$ OB = \sqrt{(-3-0)^2 + (\sqrt{7}-0)^2 } \rightarrow OB = \sqrt{16} = 4 $
$ OA^2 = a^2 \rightarrow OA = a $
$\spadesuit \, $ Menentukan nilai $ \cos AOB $
$\begin{align} AB^2 & = OA^2 + OB^2 - 2.OA.OB. \cos AOB \\ \cos AOB & = \frac{OA^2 + OB^2 - AB^2}{2.OA.OB} \\ \cos \gamma & = \frac{OA^2 + OB^2 - AB^2}{2.OA.OB} \\ \cos \gamma & = \frac{a^2 + 16 - [(a+3)^2 + 7]}{2.a.4} \\ \cos \gamma & = \frac{a^2 + 16 - [a^2 + 6a + 16]}{2.a.4} \\ \cos \gamma & = \frac{-6a}{2.a.4} = \frac{-3}{4} \end{align}$
$\spadesuit \, $ Menentukan nilai $ \sin \frac{1}{2} \gamma $
Konsep dasar : $ \cos px = 1 - 2 \sin ^2 \frac{1}{2}p x $
Sehingga : $ \cos x = 1 - 2 \sin ^2 \frac{1}{2} x $
$\begin{align} \cos \gamma & = 1 - 2 \sin ^2 \frac{1}{2} \gamma \\ \sin \frac{1}{2} \gamma & = \sqrt{\frac{1}{2} - \frac{1}{2} \cos \gamma } \\ \sin \frac{1}{2} \gamma & = \sqrt{\frac{1}{2} - \frac{1}{2} . ( \frac{-3}{4} ) } \\ \sin \frac{1}{2} \gamma & = \sqrt{\frac{7}{8}} = \sqrt{ \frac{7}{8} . \frac{2}{2}} = \frac{1}{4} \sqrt{14} \end{align}$
$\spadesuit \, $ Menentukan nilai $ \cos \frac{1}{2} ( \alpha + \beta ) \, $ pada segitiga AOB
$\begin{align} \alpha + \beta + \gamma & = 180^\circ \\ \alpha + \beta & = 180^\circ - \gamma \\ \frac{1}{2} (\alpha + \beta ) & = \frac{1}{2} (180^\circ - \gamma ) \\ \frac{1}{2} (\alpha + \beta ) & = 90^\circ - \frac{1}{2} \gamma \\ \cos \frac{1}{2} (\alpha + \beta ) & = \cos ( 90^\circ - \frac{1}{2} \gamma ) \\ & = \sin \frac{1}{2} \gamma \\ & = \frac{1}{4} \sqrt{14} \end{align}$
Jadi, nilai $ \cos \frac{1}{2} (\alpha + \beta ) = \frac{1}{4} \sqrt{14} . \heartsuit $
Cara II :
$\spadesuit \, $ Gambar
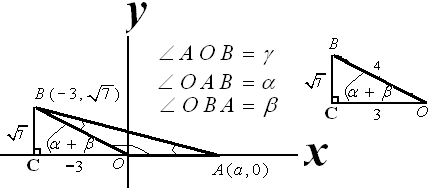
Pada segitiga BOC : $ \cos (\alpha + \beta ) = \frac{3}{4} $
$\spadesuit \, $ Konsep dasar : $ \cos px = 2 \cos ^2 \frac{1}{2}p x - 1 $
Sehingga : $ \cos x = 2 \cos ^2 \frac{1}{2} x - 1 $
$\spadesuit \, $ Menentukan sudut BOC
$\begin{align} \angle AOB & = 180^\circ - (\alpha + \beta ) \, \, \text{[dari } \Delta AOB] \\ \angle BOC + \angle AOB & = 180^\circ \, \, \, \, \text{(sudut berpelurus)} \\ \angle BOC + [ 180^\circ - (\alpha + \beta ) ] & = 180^\circ \\ \angle BOC & = (\alpha + \beta ) \end{align}$
$\spadesuit \, $ Menentukan nilai $ \cos \frac{1}{2} ( \alpha + \beta ) \, $
$\begin{align} \cos x & = 2 \cos ^2 \frac{1}{2} x - 1 \\ \cos ( \alpha + \beta ) & = 2 \cos ^2 \frac{1}{2} ( \alpha + \beta ) - 1 \\ \frac{3}{4} & = 2 \cos ^2 \frac{1}{2} ( \alpha + \beta ) - 1 \\ 2 \cos ^2 \frac{1}{2} ( \alpha + \beta ) & = \frac{7}{4} \\ \cos ^2 \frac{1}{2} ( \alpha + \beta ) & = \frac{7}{8} \\ \cos \frac{1}{2} ( \alpha + \beta ) & = \sqrt{ \frac{7}{8} } \\ \cos \frac{1}{2} ( \alpha + \beta ) & = \sqrt{ \frac{7}{8} . \frac{2}{2} } = \frac{1}{4} \sqrt{14} \end{align}$
Jadi, nilai $ \cos \frac{1}{2} (\alpha + \beta ) = \frac{1}{4} \sqrt{14} . \heartsuit $
$\spadesuit \, $ Gambar
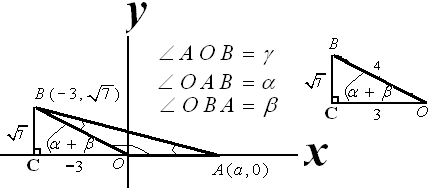
Pada segitiga BOC : $ \cos (\alpha + \beta ) = \frac{3}{4} $
$\spadesuit \, $ Konsep dasar : $ \cos px = 2 \cos ^2 \frac{1}{2}p x - 1 $
Sehingga : $ \cos x = 2 \cos ^2 \frac{1}{2} x - 1 $
$\spadesuit \, $ Menentukan sudut BOC
$\begin{align} \angle AOB & = 180^\circ - (\alpha + \beta ) \, \, \text{[dari } \Delta AOB] \\ \angle BOC + \angle AOB & = 180^\circ \, \, \, \, \text{(sudut berpelurus)} \\ \angle BOC + [ 180^\circ - (\alpha + \beta ) ] & = 180^\circ \\ \angle BOC & = (\alpha + \beta ) \end{align}$
$\spadesuit \, $ Menentukan nilai $ \cos \frac{1}{2} ( \alpha + \beta ) \, $
$\begin{align} \cos x & = 2 \cos ^2 \frac{1}{2} x - 1 \\ \cos ( \alpha + \beta ) & = 2 \cos ^2 \frac{1}{2} ( \alpha + \beta ) - 1 \\ \frac{3}{4} & = 2 \cos ^2 \frac{1}{2} ( \alpha + \beta ) - 1 \\ 2 \cos ^2 \frac{1}{2} ( \alpha + \beta ) & = \frac{7}{4} \\ \cos ^2 \frac{1}{2} ( \alpha + \beta ) & = \frac{7}{8} \\ \cos \frac{1}{2} ( \alpha + \beta ) & = \sqrt{ \frac{7}{8} } \\ \cos \frac{1}{2} ( \alpha + \beta ) & = \sqrt{ \frac{7}{8} . \frac{2}{2} } = \frac{1}{4} \sqrt{14} \end{align}$
Jadi, nilai $ \cos \frac{1}{2} (\alpha + \beta ) = \frac{1}{4} \sqrt{14} . \heartsuit $
Nomor 5
Diketahui vektor-vektor $ \vec{u} = (a,1,-a) \, $ dan $ \vec{v} = (1,a,a). \, $ Jika $ \vec{u}_1 \, $ vektor proyeksi $ \vec{u} \, $
pada $ \vec{v}, \, \vec{v}_1 \, $ vektor proyeksi $ \vec{v} \, $ pada $ \vec{u} , \, $ dan $ \theta \, $ sudut antara $ \vec{u} \, $
dan $ \vec{v} \, $ dengan $ \cos \theta = \frac{1}{3}, \, $ maka luas jajaran genjang yang dibentuk oleh $ \vec{u}_1 \, $ dan $ \vec{v}_1 \, $
adalah ....
$\clubsuit \, $ Konsep dasar
Vektor $ \vec{u} = (x_1,y_1,z_1) \, $ dan $ \vec{v} = (x_2.y_2,z_2) $
$ \vec{u} . \vec{v} = x_1.x_2 + y_1.y_2 + z_1.z_2 $
Panjang vektor :
$ | \vec{u} | = \sqrt{x_1^2 + y_1^2 + z_1^2 } \, $ dan $ | \vec{v} | = \sqrt{x_2^2 + y_2^2 + z_2^2 } \, $
$ \vec{u} . \vec{v} = |\vec{u}| |\vec{v}| \cos \theta $
Proyeksi vektor $ \vec{a} \, $ pada vektor $ \vec{b} \, $ hasilnya $ \vec{c} $
$ \vec{c} = \left( \frac{\vec{a}.\vec{b}}{|\vec{b}|^2 } \right) \vec{b} $
$\clubsuit \, $ Diketahui $ \vec{u} = (a,1,-a) \, $ dan $ \vec{v} = (1,a,a) $
$ \vec{u}.\vec{v} = a.1 + 1.a + (-a).a = 2a - a^2 $
$|\vec{u}| = \sqrt{a^2+1^2+(-a)^2} = \sqrt{1 + 2a^2} $
$|\vec{v}| = \sqrt{1^2+a^2+a^2} = \sqrt{1 + 2a^2} $
$\clubsuit \, $ Menentukan nilai $ a \, $ dengan $ \cos \theta = \frac{1}{3} $
$\begin{align} \vec{u} . \vec{v} & = |\vec{u}| |\vec{v}| \cos \theta \\ 2a - a^2 & = \sqrt{1 + 2a^2} . \sqrt{1 + 2a^2} . \frac{1}{3} \\ 6a - 3a^2 & = 1 + 2a^2 \\ 5a^2 - 6a + 1 & = 0 \\ (5a - 1)(a - 1) & = 0 \\ a = \frac{1}{5} \vee a & = 1 \end{align}$
Untuk $ a = 1 , \, $ maka $ \vec{u} = (1,1,-1) \, $ dan $ \vec{v} = (1,1,1) $
$ | \vec{u} | = \sqrt{1^2 + 1^2 + (-1)^2 } = \sqrt{3} $
$ | \vec{v} | = \sqrt{1^2 + 1^2 + 1^2 } = \sqrt{3} $
$ \vec{u} . \vec{v} = 1.1 + 1.1 + (-1).1 = 1 $
$\clubsuit \, $ Menentukan vektor $ \vec{u_1} \, $ dan $ \vec{v_1} $
$ \vec{u_1} = \left( \frac{\vec{u}.\vec{v}}{|\vec{v}|^2} \right) \vec{v} = \frac{1}{(\sqrt{3})^2} \left( \begin{matrix} 1 & 1 & 1 \end{matrix} \right) = \left( \begin{matrix} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \end{matrix} \right) $
$ \vec{v_1} = \left( \frac{\vec{u}.\vec{v}}{|\vec{u}|^2} \right) \vec{v} = \frac{1}{(\sqrt{3})^2} \left( \begin{matrix} 1 & 1 & -1 \end{matrix} \right) = \left( \begin{matrix} \frac{1}{3} & \frac{1}{3} & -\frac{1}{3} \end{matrix} \right) $
$\clubsuit \, $ Gambarnya

$ \theta \, $ adalah sudut antara $ \vec{u} \, $ dan $ \vec{v} \, $ , yang artinya $ \theta \, $ juga sudut antara $ \vec{u_1} \, $ dan $ \vec{v_1} $
Sehingga : $ \sin \theta = \frac{2\sqrt{2}}{3} $
panjang $ AB = |\vec{v}_1 | = \sqrt{\frac{1}{3}} \, $ dan $ AC = | \vec{u}_1 | = \sqrt{\frac{1}{3}} $
$\clubsuit \, $ Menentukan luas jajargenjang
$ \begin{align} L_{\Delta ABC } & = \frac{1}{2} . AB . AC . \sin \theta = \frac{1}{2}. \sqrt{\frac{1}{3}} . \sqrt{\frac{1}{3}} . \frac{2\sqrt{2}}{3} \\ & = \frac{1}{9} \sqrt{2} \end{align} $
Sehingga luas jajargenjangnya :
Luas = $ 2 \times L_{\Delta ABC} = 2 \times \frac{1}{9}\sqrt{2} = \frac{2}{9}\sqrt{2} $
Jadi, luas jajargenjangnya adalah $ \frac{2}{9}\sqrt{2} . \heartsuit $
Vektor $ \vec{u} = (x_1,y_1,z_1) \, $ dan $ \vec{v} = (x_2.y_2,z_2) $
$ \vec{u} . \vec{v} = x_1.x_2 + y_1.y_2 + z_1.z_2 $
Panjang vektor :
$ | \vec{u} | = \sqrt{x_1^2 + y_1^2 + z_1^2 } \, $ dan $ | \vec{v} | = \sqrt{x_2^2 + y_2^2 + z_2^2 } \, $
$ \vec{u} . \vec{v} = |\vec{u}| |\vec{v}| \cos \theta $
Proyeksi vektor $ \vec{a} \, $ pada vektor $ \vec{b} \, $ hasilnya $ \vec{c} $
$ \vec{c} = \left( \frac{\vec{a}.\vec{b}}{|\vec{b}|^2 } \right) \vec{b} $
$\clubsuit \, $ Diketahui $ \vec{u} = (a,1,-a) \, $ dan $ \vec{v} = (1,a,a) $
$ \vec{u}.\vec{v} = a.1 + 1.a + (-a).a = 2a - a^2 $
$|\vec{u}| = \sqrt{a^2+1^2+(-a)^2} = \sqrt{1 + 2a^2} $
$|\vec{v}| = \sqrt{1^2+a^2+a^2} = \sqrt{1 + 2a^2} $
$\clubsuit \, $ Menentukan nilai $ a \, $ dengan $ \cos \theta = \frac{1}{3} $
$\begin{align} \vec{u} . \vec{v} & = |\vec{u}| |\vec{v}| \cos \theta \\ 2a - a^2 & = \sqrt{1 + 2a^2} . \sqrt{1 + 2a^2} . \frac{1}{3} \\ 6a - 3a^2 & = 1 + 2a^2 \\ 5a^2 - 6a + 1 & = 0 \\ (5a - 1)(a - 1) & = 0 \\ a = \frac{1}{5} \vee a & = 1 \end{align}$
Untuk $ a = 1 , \, $ maka $ \vec{u} = (1,1,-1) \, $ dan $ \vec{v} = (1,1,1) $
$ | \vec{u} | = \sqrt{1^2 + 1^2 + (-1)^2 } = \sqrt{3} $
$ | \vec{v} | = \sqrt{1^2 + 1^2 + 1^2 } = \sqrt{3} $
$ \vec{u} . \vec{v} = 1.1 + 1.1 + (-1).1 = 1 $
$\clubsuit \, $ Menentukan vektor $ \vec{u_1} \, $ dan $ \vec{v_1} $
$ \vec{u_1} = \left( \frac{\vec{u}.\vec{v}}{|\vec{v}|^2} \right) \vec{v} = \frac{1}{(\sqrt{3})^2} \left( \begin{matrix} 1 & 1 & 1 \end{matrix} \right) = \left( \begin{matrix} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \end{matrix} \right) $
$ \vec{v_1} = \left( \frac{\vec{u}.\vec{v}}{|\vec{u}|^2} \right) \vec{v} = \frac{1}{(\sqrt{3})^2} \left( \begin{matrix} 1 & 1 & -1 \end{matrix} \right) = \left( \begin{matrix} \frac{1}{3} & \frac{1}{3} & -\frac{1}{3} \end{matrix} \right) $
$\clubsuit \, $ Gambarnya

$ \theta \, $ adalah sudut antara $ \vec{u} \, $ dan $ \vec{v} \, $ , yang artinya $ \theta \, $ juga sudut antara $ \vec{u_1} \, $ dan $ \vec{v_1} $
Sehingga : $ \sin \theta = \frac{2\sqrt{2}}{3} $
panjang $ AB = |\vec{v}_1 | = \sqrt{\frac{1}{3}} \, $ dan $ AC = | \vec{u}_1 | = \sqrt{\frac{1}{3}} $
$\clubsuit \, $ Menentukan luas jajargenjang
$ \begin{align} L_{\Delta ABC } & = \frac{1}{2} . AB . AC . \sin \theta = \frac{1}{2}. \sqrt{\frac{1}{3}} . \sqrt{\frac{1}{3}} . \frac{2\sqrt{2}}{3} \\ & = \frac{1}{9} \sqrt{2} \end{align} $
Sehingga luas jajargenjangnya :
Luas = $ 2 \times L_{\Delta ABC} = 2 \times \frac{1}{9}\sqrt{2} = \frac{2}{9}\sqrt{2} $
Jadi, luas jajargenjangnya adalah $ \frac{2}{9}\sqrt{2} . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.