Nomor 1
Misalkan titik A dan B pada lingkaran $ x^2 + y^2 - 6x - 2y + k = 0 \, $ sehingga garis singgung lingkaran di titik A dan B
berpotongan di titik C(8,1). Jika luas segiempat yang melalui A, B, C, dan pusat lingkaran adalah 12, maka $ k = .... $
Cara I :
$\clubsuit \, $ Konsep dasar lingkaran :
*). Persamaan lingkaran : $ x^2 + y^2 + Ax + By + C = 0 $
Pusatnya : $ (a,b)= \left( -\frac{A}{2}, - \frac{B}{2} \right) $
Jari-jarinya : $ r^2 = a^2 + b^2 - C $
$\clubsuit \, $ Persamaan garis singgung lingkaran di titik ($x_1,y_1$)
$ x_1.x + y_1.y + A \frac{(x_1+x)}{2} + B\frac{(y_1+y)}{2} + C = 0 $
$\clubsuit \, $ Jarak titik ($x_1,y_1$) dan ($x_2,y_2$) : Jarak $ = \sqrt{(x_2 - x_1)^2 + (y_2-y_1)^2 } $
$\clubsuit \, $ Menentukan unsur-unsur lingkaran :
$ x^2 + y^2 - 6x - 2y + k = 0 \rightarrow A = -6, \, B = -2, \, C = k $
Pusat lingkaran : $ (a,b)= \left( -\frac{-6}{2}, - \frac{-2}{2} \right) = (3,1) $
Jari-jari : $ r^2 = a^2 + b^2 - C \rightarrow r^2 = 3^2 + 1^2 - k \rightarrow r^2 = 10 - k \, $ ....pers(i)
Gambar ilustrasinya :

Panjang $ OC = 5 $
$\clubsuit \, $ Menentukan titik A($x_1,y_1$)
*). Segitiga AOC dan segitiga BOC kongruen sehingga luas segiempat AOBC adalah 2 kali segitiga AOC.
$ \begin{align} \text{Luas segiempat } AOBC & = 12 \\ 2 \times \text{Luas } AOC & = 12 \\ \text{Luas } AOC & = 6 \\ \frac{1}{2}.OC.AD & = 6 \\ \frac{1}{2}.5.AD & = 6 \\ AD & = \frac{12}{5} \end{align} $
Sehingga $ y_1 = AD + 1 = \frac{12}{5} + 1 = \frac{17}{5} $
*). Persamaan garis singgung pada titik A($x_1,y_1$) dan melalui titik (8,1). Substitusi titik (8,1)
$ \begin{align} x_1.x + y_1.y -6. \frac{(x_1+x)}{2} -2.\frac{(y_1+y)}{2} + k & = 0 \\ x_1.x + y_1.y -3 (x_1+x) -(y_1+y) + k & = 0 \, \, \, \, \, \text{(substitusi (8,1))} \\ x_1.8 + y_1.1 -3 (x_1+8) -(y_1+1) + k & = 0 \\ 8x_1 + y_1 -3 x_1-24 -y_1 - 1 + k & = 0 \\ 5x_1 - 25 + k & = 0 \\ x_1 & = \frac{25-k}{5} \end{align} $
Sehingga titik A adalah $ A(x_1,y_1) = A\left( \frac{25-k}{5}, \frac{17}{5} \right) $
$\clubsuit \, $ Jari-jari lingkaran adalah OA ($r = |OA|$)
$ \begin{align} |OA| & = \sqrt{(x_1-3)^2 + (y_1-1)^2} \\ |OA| & = \sqrt{(\frac{25-k}{5}-3)^2 + (\frac{17}{5}-1)^2} \\ |OA| & = \sqrt{(\frac{10-k}{5})^2 + (\frac{12}{5})^2} \\ |OA|^2 & = (\frac{10-k}{5})^2 + (\frac{12}{5})^2 \end{align} $
$\clubsuit \, $ Menentukan nilai $ k \, $ dari pers(i) :
$ \begin{align} |OA| & = r \, \, \, \, \, \text{(kuadratkan)} \\ |OA|^2 & = r^2 \\ (\frac{10-k}{5})^2 + (\frac{12}{5})^2 & = 10 - k \\ \frac{k^2 - 20k + 100}{25} + \frac{144}{25} & = 10 - k \, \, \, \, \, \text{(kali 25)} \\ k^2 - 20k + 100 + 144 & = 250 - 25k \\ k^2 + 5k - 6 & = 0 \\ (k-1)(k+6) & = 0 \\ k = 1 \vee k & = -6 \end{align} $
Jadi, nilai $ k = 1 . \heartsuit $
$\clubsuit \, $ Konsep dasar lingkaran :
*). Persamaan lingkaran : $ x^2 + y^2 + Ax + By + C = 0 $
Pusatnya : $ (a,b)= \left( -\frac{A}{2}, - \frac{B}{2} \right) $
Jari-jarinya : $ r^2 = a^2 + b^2 - C $
$\clubsuit \, $ Persamaan garis singgung lingkaran di titik ($x_1,y_1$)
$ x_1.x + y_1.y + A \frac{(x_1+x)}{2} + B\frac{(y_1+y)}{2} + C = 0 $
$\clubsuit \, $ Jarak titik ($x_1,y_1$) dan ($x_2,y_2$) : Jarak $ = \sqrt{(x_2 - x_1)^2 + (y_2-y_1)^2 } $
$\clubsuit \, $ Menentukan unsur-unsur lingkaran :
$ x^2 + y^2 - 6x - 2y + k = 0 \rightarrow A = -6, \, B = -2, \, C = k $
Pusat lingkaran : $ (a,b)= \left( -\frac{-6}{2}, - \frac{-2}{2} \right) = (3,1) $
Jari-jari : $ r^2 = a^2 + b^2 - C \rightarrow r^2 = 3^2 + 1^2 - k \rightarrow r^2 = 10 - k \, $ ....pers(i)
Gambar ilustrasinya :

Panjang $ OC = 5 $
$\clubsuit \, $ Menentukan titik A($x_1,y_1$)
*). Segitiga AOC dan segitiga BOC kongruen sehingga luas segiempat AOBC adalah 2 kali segitiga AOC.
$ \begin{align} \text{Luas segiempat } AOBC & = 12 \\ 2 \times \text{Luas } AOC & = 12 \\ \text{Luas } AOC & = 6 \\ \frac{1}{2}.OC.AD & = 6 \\ \frac{1}{2}.5.AD & = 6 \\ AD & = \frac{12}{5} \end{align} $
Sehingga $ y_1 = AD + 1 = \frac{12}{5} + 1 = \frac{17}{5} $
*). Persamaan garis singgung pada titik A($x_1,y_1$) dan melalui titik (8,1). Substitusi titik (8,1)
$ \begin{align} x_1.x + y_1.y -6. \frac{(x_1+x)}{2} -2.\frac{(y_1+y)}{2} + k & = 0 \\ x_1.x + y_1.y -3 (x_1+x) -(y_1+y) + k & = 0 \, \, \, \, \, \text{(substitusi (8,1))} \\ x_1.8 + y_1.1 -3 (x_1+8) -(y_1+1) + k & = 0 \\ 8x_1 + y_1 -3 x_1-24 -y_1 - 1 + k & = 0 \\ 5x_1 - 25 + k & = 0 \\ x_1 & = \frac{25-k}{5} \end{align} $
Sehingga titik A adalah $ A(x_1,y_1) = A\left( \frac{25-k}{5}, \frac{17}{5} \right) $
$\clubsuit \, $ Jari-jari lingkaran adalah OA ($r = |OA|$)
$ \begin{align} |OA| & = \sqrt{(x_1-3)^2 + (y_1-1)^2} \\ |OA| & = \sqrt{(\frac{25-k}{5}-3)^2 + (\frac{17}{5}-1)^2} \\ |OA| & = \sqrt{(\frac{10-k}{5})^2 + (\frac{12}{5})^2} \\ |OA|^2 & = (\frac{10-k}{5})^2 + (\frac{12}{5})^2 \end{align} $
$\clubsuit \, $ Menentukan nilai $ k \, $ dari pers(i) :
$ \begin{align} |OA| & = r \, \, \, \, \, \text{(kuadratkan)} \\ |OA|^2 & = r^2 \\ (\frac{10-k}{5})^2 + (\frac{12}{5})^2 & = 10 - k \\ \frac{k^2 - 20k + 100}{25} + \frac{144}{25} & = 10 - k \, \, \, \, \, \text{(kali 25)} \\ k^2 - 20k + 100 + 144 & = 250 - 25k \\ k^2 + 5k - 6 & = 0 \\ (k-1)(k+6) & = 0 \\ k = 1 \vee k & = -6 \end{align} $
Jadi, nilai $ k = 1 . \heartsuit $
Cara II :
$\clubsuit \, $ Konsep dasar lingkaran :
*). Persamaan lingkaran : $ x^2 + y^2 + Ax + By + C = 0 $
Pusatnya : $ (a,b)= \left( -\frac{A}{2}, - \frac{B}{2} \right) $
Jari-jarinya : $ r^2 = a^2 + b^2 - C $
$\clubsuit \, $ Menentukan unsur-unsur lingkaran :
$ x^2 + y^2 - 6x - 2y + k = 0 \rightarrow A = -6, \, B = -2, \, C = k $
Pusat lingkaran : $ (a,b)= \left( -\frac{-6}{2}, - \frac{-2}{2} \right) = (3,1) $
Jari-jari : $ r^2 = a^2 + b^2 - C \rightarrow r^2 = 3^2 + 1^2 - k \rightarrow k = 10 - r^2 \, $ ....pers(i)
Gambar ilustrasinya :

Panjang $ OC = 5 $
$\clubsuit \, $ Teorema Pythagoras pada segitiga AOC
$ \begin{align} OC^2 & = AO^2 + AC^2 \\ 5^2 & = r^2 + AC^2 \\ AC^2 & = 25 - r^2 \\ AC & = \sqrt{25 - r^2} \end{align} $
$\clubsuit \, $ Segitiga AOC dan segitiga BOC kongruen sehingga luas segiempat AOBC adalah 2 kali segitiga AOC.
$ \begin{align} \text{Luas segiempat } AOBC & = 12 \\ 2 \times \text{Luas } AOC & = 12 \\ \text{Luas } AOC & = 6 \\ \frac{1}{2}.OA.AC & = 6 \\ r.\sqrt{25 - r^2} & = 12 \, \, \, \, \text{(kuadratkan)} \\ r^2.(25 - r^2) & = 144 \\ r^4 - 25r^2 + 144 & = 0 \\ (r^2 - 9)(r^2 -16) & = 0 \\ r^2 = 9 \vee r^2 & = 16 \end{align} $
$\clubsuit \, $ Menentukan nilai $ k \, $ dari nilai $ r^2 \, $ dan pers(i) :
$ \begin{align} r^2 = 9 \rightarrow k & = 10 - r^2 \\ k & = 10 - 9 = 1 \\ r^2 = 16 \rightarrow k & = 10 - r^2 \\ k & = 10 - 16 = -6 \end{align} $
Jadi, nilai $ k = 1 . \heartsuit $
$\clubsuit \, $ Konsep dasar lingkaran :
*). Persamaan lingkaran : $ x^2 + y^2 + Ax + By + C = 0 $
Pusatnya : $ (a,b)= \left( -\frac{A}{2}, - \frac{B}{2} \right) $
Jari-jarinya : $ r^2 = a^2 + b^2 - C $
$\clubsuit \, $ Menentukan unsur-unsur lingkaran :
$ x^2 + y^2 - 6x - 2y + k = 0 \rightarrow A = -6, \, B = -2, \, C = k $
Pusat lingkaran : $ (a,b)= \left( -\frac{-6}{2}, - \frac{-2}{2} \right) = (3,1) $
Jari-jari : $ r^2 = a^2 + b^2 - C \rightarrow r^2 = 3^2 + 1^2 - k \rightarrow k = 10 - r^2 \, $ ....pers(i)
Gambar ilustrasinya :

Panjang $ OC = 5 $
$\clubsuit \, $ Teorema Pythagoras pada segitiga AOC
$ \begin{align} OC^2 & = AO^2 + AC^2 \\ 5^2 & = r^2 + AC^2 \\ AC^2 & = 25 - r^2 \\ AC & = \sqrt{25 - r^2} \end{align} $
$\clubsuit \, $ Segitiga AOC dan segitiga BOC kongruen sehingga luas segiempat AOBC adalah 2 kali segitiga AOC.
$ \begin{align} \text{Luas segiempat } AOBC & = 12 \\ 2 \times \text{Luas } AOC & = 12 \\ \text{Luas } AOC & = 6 \\ \frac{1}{2}.OA.AC & = 6 \\ r.\sqrt{25 - r^2} & = 12 \, \, \, \, \text{(kuadratkan)} \\ r^2.(25 - r^2) & = 144 \\ r^4 - 25r^2 + 144 & = 0 \\ (r^2 - 9)(r^2 -16) & = 0 \\ r^2 = 9 \vee r^2 & = 16 \end{align} $
$\clubsuit \, $ Menentukan nilai $ k \, $ dari nilai $ r^2 \, $ dan pers(i) :
$ \begin{align} r^2 = 9 \rightarrow k & = 10 - r^2 \\ k & = 10 - 9 = 1 \\ r^2 = 16 \rightarrow k & = 10 - r^2 \\ k & = 10 - 16 = -6 \end{align} $
Jadi, nilai $ k = 1 . \heartsuit $
Nomor 2
Jika $ \sin \left( x + 15^\circ \right) = a \, $ dengan $ 0^\circ \leq x \leq 15^\circ , \, $ maka nilai
$ \sin \left( 2x + 60^\circ \right) \, $ adalah ....
$\spadesuit \, $ Konsep dasar trigonometri
$ \sin (A+B) = \sin A \cos B + \cos A \sin B $
$ \sin 2A = 2 \sin A \cos A $
$\spadesuit \, $ Menentukan nilai trigonometri
$ \sin (x+15^\circ ) = a \rightarrow \sin (x+15^\circ ) = \frac{a}{1} = \frac{de}{mi} $
gambar segitiga untuk sudut $ (x+15^\circ ) $ :

sehingga nilai $ \cos (x+15^\circ ) = \frac{sa}{mi} = \frac{\sqrt{1-a^2}}{1} = \sqrt{1-a^2} $
*). Nilai $ \sin 2(x+15^\circ ) $
$\begin{align} \sin 2(x+15^\circ ) & = 2 \sin (x+15^\circ ) . \cos (x+15^\circ ) \\ \sin 2(x+15^\circ ) & = 2 a \sqrt{1-a^2} \end{align}$
gambar segitiga untuk sudut $ 2(x+15^\circ ) $ :
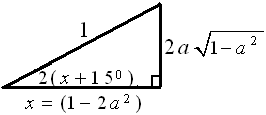
Cara menentukan nilai $ x $
$\begin{align} x^2 & = 1^2 - (2 a \sqrt{1-a^2})^2 \\ x & = \sqrt{1^2 - (2 a \sqrt{1-a^2})^2 } \\ x & = \sqrt{1 - (4 a^2(1-a^2)) } \\ & = \sqrt{1 - (4 a^2 - 4a^4) } \\ & = \sqrt{1 - 4 a^2 + 4a^4 } \\ & = \sqrt{(1-2a^2)^2 } \\ x & = 1-2a^2 \end{align}$
sehingga nilai $ \cos 2(x+15^\circ ) = \frac{samping}{miring} = \frac{1-2a^2}{1} = 1-2a^2 $
$\spadesuit \, $ Menentukan nilai $ \sin \left( 2x + 60^\circ \right) \, $ dan gunakan $ \sin (A+B) $
$\begin{align} \sin \left( 2x + 60^\circ \right) & = \sin \left( 2x + 30^\circ + 30^\circ \right) \\ & = \sin \left( \underbrace{2(x + 15^\circ )}_{A} + \underbrace{30^\circ }_{B} \right) \\ & = \sin A \cos B + \cos A \sin B \\ & = \sin 2(x + 15^\circ ) \cos 30^\circ + \cos 2(x + 15^\circ ) \sin 30^\circ \\ & = 2 a \sqrt{1-a^2} . \frac{1}{2} \sqrt{3} + (1-2a^2) . \frac{1}{2} \\ & = a \sqrt{1-a^2} \sqrt{3} + \frac{1}{2} - a^2 \\ & = a \sqrt{3(1-a^2)} + \frac{1}{2} - a^2 \\ & = \frac{1}{2} - a^2 + a \sqrt{3(1-a^2)} \end{align}$
Jadi, nilai $ \sin \left( 2x + 60^\circ \right) = \frac{1}{2} - a^2 + a \sqrt{3(1-a^2)} . \, \heartsuit $
$ \sin (A+B) = \sin A \cos B + \cos A \sin B $
$ \sin 2A = 2 \sin A \cos A $
$\spadesuit \, $ Menentukan nilai trigonometri
$ \sin (x+15^\circ ) = a \rightarrow \sin (x+15^\circ ) = \frac{a}{1} = \frac{de}{mi} $
gambar segitiga untuk sudut $ (x+15^\circ ) $ :

sehingga nilai $ \cos (x+15^\circ ) = \frac{sa}{mi} = \frac{\sqrt{1-a^2}}{1} = \sqrt{1-a^2} $
*). Nilai $ \sin 2(x+15^\circ ) $
$\begin{align} \sin 2(x+15^\circ ) & = 2 \sin (x+15^\circ ) . \cos (x+15^\circ ) \\ \sin 2(x+15^\circ ) & = 2 a \sqrt{1-a^2} \end{align}$
gambar segitiga untuk sudut $ 2(x+15^\circ ) $ :
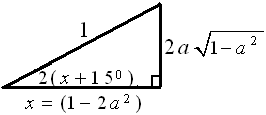
Cara menentukan nilai $ x $
$\begin{align} x^2 & = 1^2 - (2 a \sqrt{1-a^2})^2 \\ x & = \sqrt{1^2 - (2 a \sqrt{1-a^2})^2 } \\ x & = \sqrt{1 - (4 a^2(1-a^2)) } \\ & = \sqrt{1 - (4 a^2 - 4a^4) } \\ & = \sqrt{1 - 4 a^2 + 4a^4 } \\ & = \sqrt{(1-2a^2)^2 } \\ x & = 1-2a^2 \end{align}$
sehingga nilai $ \cos 2(x+15^\circ ) = \frac{samping}{miring} = \frac{1-2a^2}{1} = 1-2a^2 $
$\spadesuit \, $ Menentukan nilai $ \sin \left( 2x + 60^\circ \right) \, $ dan gunakan $ \sin (A+B) $
$\begin{align} \sin \left( 2x + 60^\circ \right) & = \sin \left( 2x + 30^\circ + 30^\circ \right) \\ & = \sin \left( \underbrace{2(x + 15^\circ )}_{A} + \underbrace{30^\circ }_{B} \right) \\ & = \sin A \cos B + \cos A \sin B \\ & = \sin 2(x + 15^\circ ) \cos 30^\circ + \cos 2(x + 15^\circ ) \sin 30^\circ \\ & = 2 a \sqrt{1-a^2} . \frac{1}{2} \sqrt{3} + (1-2a^2) . \frac{1}{2} \\ & = a \sqrt{1-a^2} \sqrt{3} + \frac{1}{2} - a^2 \\ & = a \sqrt{3(1-a^2)} + \frac{1}{2} - a^2 \\ & = \frac{1}{2} - a^2 + a \sqrt{3(1-a^2)} \end{align}$
Jadi, nilai $ \sin \left( 2x + 60^\circ \right) = \frac{1}{2} - a^2 + a \sqrt{3(1-a^2)} . \, \heartsuit $
Nomor 3
Diketahui $\vec{a} = 2\vec{i} - 2\vec{j} - \vec{k} \, $ dan $ \vec{b} = \vec{i} - 4\vec{j}. \, $ Luas jajaran genjang yang dibentuk
oleh $ \vec{a} + \vec{b} \, $ dan $ \vec{a} \, $ adalah ....
$\clubsuit \, $ Konsep dasar vektor :
*). Misalkan ada vektor $ \vec{a} = (a_1, a_2, a_3) \, $ dan $ \vec{b} = (b_1,b_2,b_3) $
i).Penjumlahan : $ \vec{a} + \vec{b} = (a_1 + b_1, a_2 + b_2, a_3 + b_3) $
ii).Perkalian dot : $ \vec{a} . \vec{b} = a_1. b_1 + a_2 . b_2 + a_3 . b_3 $
iii).Panjang vektor : $ |\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2 } $
iv). Sudut dua vektor : $ \cos \theta = \frac{\vec{a}.\vec{b}}{|\vec{a}|.|\vec{b}|} $
$\clubsuit \, $ Konsep Luas pada segitiga ABC
Luas segitiga ABC = $ \frac{1}{2} . AB. AC. \sin A $
$\clubsuit \, $ Diketahui vektor-vektor berikut :
$ \vec{a} = 2\vec{i} - 2\vec{j} - \vec{k} \rightarrow \vec{a} = (2, - 2, - 1) $
$ \vec{b} = \vec{i} - 4\vec{j} \rightarrow \vec{b} = (1, -4, 0 ) $
$ \vec{c} = \vec{a} + \vec{b} = (3, -6, -1) $
$ \vec{a} . \vec{c} = 2.3 + (-2).(-6) + (-1).(-1) = 6 +12 + 1 = 19 $
$ |\vec{a}| = \sqrt{2^2 + (-3)^2 + (-1)^2 } = \sqrt{9} = 3 $
$ |\vec{c}| = \sqrt{3^2 + (-6)^2 + (-1)^2 } = \sqrt{46} $
$\clubsuit \, $ Menentukan besarnya sudut $ \vec{a} \, $ dan $ \vec{c} $
$ \cos \theta = \frac{\vec{a}.\vec{c}}{|\vec{a}|.|\vec{c}|} = \frac{19}{3.\sqrt{46}} \rightarrow \cos \theta = \frac{19}{3\sqrt{46}} $
gambar segitganya :

Sehingga nilai $ \sin \theta = \frac{\sqrt{53}}{3\sqrt{46}} $
$\clubsuit \, $ Gambar jajargenjang yang dibentuk oleh $ \vec{c} = \vec{a} + \vec{b} \, $ dan $ \vec{a} $
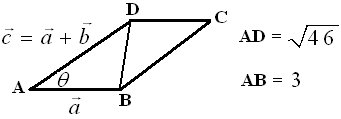
$\clubsuit \, $ Menentukan luas jajargenjang
$\begin{align} \text{ Luas jajargenjang } & = 2 L_{\Delta ABD} \\ & = 2 . \frac{1}{2} . AB . AD . \sin \theta \\ & = AB. AD . \sin \theta \\ & = 3. \sqrt{46} . \frac{\sqrt{53}}{3\sqrt{46}} \\ & = \sqrt{53} \end{align}$
Jadi, luas jajargenjang adalah $ \sqrt{53} . \, \heartsuit $
*). Misalkan ada vektor $ \vec{a} = (a_1, a_2, a_3) \, $ dan $ \vec{b} = (b_1,b_2,b_3) $
i).Penjumlahan : $ \vec{a} + \vec{b} = (a_1 + b_1, a_2 + b_2, a_3 + b_3) $
ii).Perkalian dot : $ \vec{a} . \vec{b} = a_1. b_1 + a_2 . b_2 + a_3 . b_3 $
iii).Panjang vektor : $ |\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2 } $
iv). Sudut dua vektor : $ \cos \theta = \frac{\vec{a}.\vec{b}}{|\vec{a}|.|\vec{b}|} $
$\clubsuit \, $ Konsep Luas pada segitiga ABC
Luas segitiga ABC = $ \frac{1}{2} . AB. AC. \sin A $
$\clubsuit \, $ Diketahui vektor-vektor berikut :
$ \vec{a} = 2\vec{i} - 2\vec{j} - \vec{k} \rightarrow \vec{a} = (2, - 2, - 1) $
$ \vec{b} = \vec{i} - 4\vec{j} \rightarrow \vec{b} = (1, -4, 0 ) $
$ \vec{c} = \vec{a} + \vec{b} = (3, -6, -1) $
$ \vec{a} . \vec{c} = 2.3 + (-2).(-6) + (-1).(-1) = 6 +12 + 1 = 19 $
$ |\vec{a}| = \sqrt{2^2 + (-3)^2 + (-1)^2 } = \sqrt{9} = 3 $
$ |\vec{c}| = \sqrt{3^2 + (-6)^2 + (-1)^2 } = \sqrt{46} $
$\clubsuit \, $ Menentukan besarnya sudut $ \vec{a} \, $ dan $ \vec{c} $
$ \cos \theta = \frac{\vec{a}.\vec{c}}{|\vec{a}|.|\vec{c}|} = \frac{19}{3.\sqrt{46}} \rightarrow \cos \theta = \frac{19}{3\sqrt{46}} $
gambar segitganya :

Sehingga nilai $ \sin \theta = \frac{\sqrt{53}}{3\sqrt{46}} $
$\clubsuit \, $ Gambar jajargenjang yang dibentuk oleh $ \vec{c} = \vec{a} + \vec{b} \, $ dan $ \vec{a} $

$\clubsuit \, $ Menentukan luas jajargenjang
$\begin{align} \text{ Luas jajargenjang } & = 2 L_{\Delta ABD} \\ & = 2 . \frac{1}{2} . AB . AD . \sin \theta \\ & = AB. AD . \sin \theta \\ & = 3. \sqrt{46} . \frac{\sqrt{53}}{3\sqrt{46}} \\ & = \sqrt{53} \end{align}$
Jadi, luas jajargenjang adalah $ \sqrt{53} . \, \heartsuit $
Nomor 4
Pencerminan garis $ y = -x + 2 \, $ terhadap garis $ y = 3 \, $ menghasilkan garis ....
$\spadesuit \, $ Konsep dasar pencerminan (refleksi)
Titik ($x,y$) dicerminkan terhadap garis $ y = m , \, $ bayangannya ($x^\prime , y^\prime$) :
$ (x^\prime , y^\prime) = ( x, 2m-y) $
artinya $ x^\prime = x, \, $ dan $ y^\prime = 2m - y $
$\spadesuit \, $ Karena yang ditransformasi (dicerminkan) adalah garis (suatu persamaan), maka cukup kita transformasi titik ($x,y$) saja (ini berlaku umum untuk semua jenis transformasi).
$\spadesuit \, $ Pencerminan terhadap garis $ y = 3 $
$\begin{align} (x^\prime , y^\prime) & = ( x, 2m-y) \\ (x^\prime , y^\prime) & = ( x, 2.3-y) \\ (x^\prime , y^\prime) & = ( x, 6-y) \end{align}$
diperoleh $ x^\prime = x, \, $ dan $ y^\prime = 6-y \rightarrow y = 6 - y^\prime $
$\spadesuit \, $ Menentukan bayangan dengan substitusi $ x = x^\prime \, $ dan $ y = 6 - y^\prime $
Persamaan awal : $ y = -x + 2 $
$\begin{align} \text{bayangan : } 6 - y^\prime & = -x^\prime + 2 \\ y^\prime & = x^\prime + 4 \end{align}$
Jadi, bayangannya adalah $ y = x + 4 . \, \heartsuit $
Titik ($x,y$) dicerminkan terhadap garis $ y = m , \, $ bayangannya ($x^\prime , y^\prime$) :
$ (x^\prime , y^\prime) = ( x, 2m-y) $
artinya $ x^\prime = x, \, $ dan $ y^\prime = 2m - y $
$\spadesuit \, $ Karena yang ditransformasi (dicerminkan) adalah garis (suatu persamaan), maka cukup kita transformasi titik ($x,y$) saja (ini berlaku umum untuk semua jenis transformasi).
$\spadesuit \, $ Pencerminan terhadap garis $ y = 3 $
$\begin{align} (x^\prime , y^\prime) & = ( x, 2m-y) \\ (x^\prime , y^\prime) & = ( x, 2.3-y) \\ (x^\prime , y^\prime) & = ( x, 6-y) \end{align}$
diperoleh $ x^\prime = x, \, $ dan $ y^\prime = 6-y \rightarrow y = 6 - y^\prime $
$\spadesuit \, $ Menentukan bayangan dengan substitusi $ x = x^\prime \, $ dan $ y = 6 - y^\prime $
Persamaan awal : $ y = -x + 2 $
$\begin{align} \text{bayangan : } 6 - y^\prime & = -x^\prime + 2 \\ y^\prime & = x^\prime + 4 \end{align}$
Jadi, bayangannya adalah $ y = x + 4 . \, \heartsuit $
Nomor 5
Pada kubus ABCD.EFGH dengan panjang rusuk 4, titik P terletak pada segmen AF sehingga PF = 2AP. Titik Q adalah titik potong garis
GP dan bidang ABCD. Jika $ \alpha \, $ adalah sudut yang terbentuk antara garis GQ dan garis DA, maka nilai $ \cos \alpha \, $ adalah ....
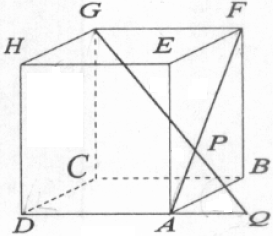

$\clubsuit \, $ Menentukan unsur-unsur kubus dengan panjang rusuk kubus : $ s = 4 $
*). Panjang AF = diagonal sisi = $ s\sqrt{2} = 4\sqrt{2} $
*). PF = 2AP $ \rightarrow \frac{PF}{AP} = \frac{2}{1} $
sehingga $ AP = \frac{1}{3} AF = \frac{1}{3} . 4\sqrt{2} = \frac{4\sqrt{2}}{3} $
*).Panjang AQ dari segitiga berikut,

Segitiga APQ sebangun dengan segitiga GDQ :
$\begin{align} \frac{AQ}{DQ} & = \frac{AP}{DG} \\ \frac{x}{x + 4} & = \frac{\frac{1}{3}4\sqrt{2}}{4\sqrt{2}} \\ \frac{x}{x + 4} & = \frac{1}{3} \\ 3x & = x + 4 \\ x & = 2 \\ GQ & = \sqrt{DQ^2 + GD^2 } \\ GQ & = \sqrt{6^2 + (4\sqrt{2})^2 } \\ GQ & = \sqrt{36 + 32 } \\ GQ & = \sqrt{68 } = 2\sqrt{17} \end{align}$
$\clubsuit \, $ Menentukan nilai $ \cos \alpha \, $ dari segitiga GDQ
$\begin{align} \cos \alpha = \frac{samping}{miring} = \frac{6}{2\sqrt{17}} = \frac{3}{\sqrt{17}} \end{align}$
Jadi, nilai $ \cos \alpha = \frac{3}{\sqrt{17}} . \, \heartsuit$
*). Panjang AF = diagonal sisi = $ s\sqrt{2} = 4\sqrt{2} $
*). PF = 2AP $ \rightarrow \frac{PF}{AP} = \frac{2}{1} $
sehingga $ AP = \frac{1}{3} AF = \frac{1}{3} . 4\sqrt{2} = \frac{4\sqrt{2}}{3} $
*).Panjang AQ dari segitiga berikut,

Segitiga APQ sebangun dengan segitiga GDQ :
$\begin{align} \frac{AQ}{DQ} & = \frac{AP}{DG} \\ \frac{x}{x + 4} & = \frac{\frac{1}{3}4\sqrt{2}}{4\sqrt{2}} \\ \frac{x}{x + 4} & = \frac{1}{3} \\ 3x & = x + 4 \\ x & = 2 \\ GQ & = \sqrt{DQ^2 + GD^2 } \\ GQ & = \sqrt{6^2 + (4\sqrt{2})^2 } \\ GQ & = \sqrt{36 + 32 } \\ GQ & = \sqrt{68 } = 2\sqrt{17} \end{align}$
$\clubsuit \, $ Menentukan nilai $ \cos \alpha \, $ dari segitiga GDQ
$\begin{align} \cos \alpha = \frac{samping}{miring} = \frac{6}{2\sqrt{17}} = \frac{3}{\sqrt{17}} \end{align}$
Jadi, nilai $ \cos \alpha = \frac{3}{\sqrt{17}} . \, \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.