Nomor 1
Pernyataan yang mempunyai nilai kebenaran sama dengan pernyataan : "Jika bilangan ganjil sama dengan bilangan genap, maka 1 + 2 bilangan
ganjil" adalah ...
$\clubsuit \, $ Untuk implikasi, $B \Rightarrow S \,$ nilainya $S$ , selain itu $B$ .
Ket : B = Benar dan S = Salah.
$\clubsuit \, $ Cek nilai kebenaran soal :
bilangan ganjil sama dengan bilangan genap : nilainya S (salah)
1 + 2 bilangan ganjil : nilainya B (benar)
"Jika bilangan ganjil sama dengan bilangan genap, maka 1 + 2 bilangan ganjil"
sehingga : $S \Rightarrow B \,$ nilainya B (benar) . Artinya nilai kebenaran soal adalah B (benar).
Kita harus mencari di opsi yang nilai kebenarannya B juga, yaitu opsi D .
"Jika bilangan ganjil sama dengan bilangan genap, maka 1 + 2 bilangan genap"
$S \Rightarrow S \,$ nilai kebenarannya B (benar) juga.
Jadi, nilai kebenaran yang sama adalah opsi D.$\heartsuit $
Ket : B = Benar dan S = Salah.
$\clubsuit \, $ Cek nilai kebenaran soal :
bilangan ganjil sama dengan bilangan genap : nilainya S (salah)
1 + 2 bilangan ganjil : nilainya B (benar)
"Jika bilangan ganjil sama dengan bilangan genap, maka 1 + 2 bilangan ganjil"
sehingga : $S \Rightarrow B \,$ nilainya B (benar) . Artinya nilai kebenaran soal adalah B (benar).
Kita harus mencari di opsi yang nilai kebenarannya B juga, yaitu opsi D .
"Jika bilangan ganjil sama dengan bilangan genap, maka 1 + 2 bilangan genap"
$S \Rightarrow S \,$ nilai kebenarannya B (benar) juga.
Jadi, nilai kebenaran yang sama adalah opsi D.$\heartsuit $
Nomor 2
Jika $n$ memenuhi
$\underbrace{25^{0,25}\times 25^{0,25}\times ...\times 25^{0,25}}_{n \text{ faktor}}=125,$
maka $(n-3)(n+2)= ...$
maka $(n-3)(n+2)= ...$
$\spadesuit \, $ Rumus Dasar :
$(a^m)^n = a^{m.n} \, $ dan $\, a^m.a^n = a^{m+n}$
$a^{f(x)} = a^{g(x)} \Rightarrow f(x) = g(x) $
$\spadesuit \, $ Menentukan nilai $n$
$\begin{align} \underbrace{25^{0,25}\times 25^{0,25}\times ...\times 25^{0,25}}_{n \text{ faktor}} & =125 \\ \underbrace{(5^2)^{\frac{1}{4}}\times (5^2)^{\frac{1}{4}}\times ...\times (5^2)^{\frac{1}{4}}}_{n \text{ faktor}} & =125 \\ \underbrace{5^{\frac{1}{2}}\times 5^{\frac{1}{2}}\times ...\times 5^{\frac{1}{2}}}_{n \text{ faktor}} & =125 \\ 5^ {\underbrace{{\frac{1}{2}} + {\frac{1}{2}} + ...+ {\frac{1}{2}}}_{n \text{ faktor}} } & = 5^3 \\ 5^{\frac{1}{2}n} & = 5^3 \\ \frac{1}{2}n & = 3 \\ n & = 6 \end{align}$
Sehingga : $(n-3)(n+2) = (6-3)(6+2) = 3 . 8 = 24$
Jadi, nilai $(n-3)(n+2) = 24 . \heartsuit $
$(a^m)^n = a^{m.n} \, $ dan $\, a^m.a^n = a^{m+n}$
$a^{f(x)} = a^{g(x)} \Rightarrow f(x) = g(x) $
$\spadesuit \, $ Menentukan nilai $n$
$\begin{align} \underbrace{25^{0,25}\times 25^{0,25}\times ...\times 25^{0,25}}_{n \text{ faktor}} & =125 \\ \underbrace{(5^2)^{\frac{1}{4}}\times (5^2)^{\frac{1}{4}}\times ...\times (5^2)^{\frac{1}{4}}}_{n \text{ faktor}} & =125 \\ \underbrace{5^{\frac{1}{2}}\times 5^{\frac{1}{2}}\times ...\times 5^{\frac{1}{2}}}_{n \text{ faktor}} & =125 \\ 5^ {\underbrace{{\frac{1}{2}} + {\frac{1}{2}} + ...+ {\frac{1}{2}}}_{n \text{ faktor}} } & = 5^3 \\ 5^{\frac{1}{2}n} & = 5^3 \\ \frac{1}{2}n & = 3 \\ n & = 6 \end{align}$
Sehingga : $(n-3)(n+2) = (6-3)(6+2) = 3 . 8 = 24$
Jadi, nilai $(n-3)(n+2) = 24 . \heartsuit $
Nomor 3
Persamaan $x^2-ax-(a+1)=0 \, $ mempunyai akar-akar $x_1 > 1 $ dan $x_2 < 1 $ untuk ...
$\clubsuit \, $ Jumlah akar dan kali akar
$x_1+x_2 = \frac{-b}{a} = \frac{-(-a)}{1} = a$
$x_1.x_2 = \frac{c}{a} = \frac{-(a+1)}{1} = -(a+1)$
$\clubsuit \, $ Memodifikasi dan dikalikan
$x_1 > 1 \Rightarrow x_1 - 1 > 0 \, \, \text{(positif)}$
$x_2 < 1 \Rightarrow x_2 - 1 < 0 \, \, \text{(negatif)}$
$\begin{align*} (x_1-1)(x_2-1) & < 0 \, \, \text{(positif kali negatif = negatif)}\\ x_1.x_2 - (x_1+x_2) + 1 & < 0 \\ -(a+1)-(a) + 1 & < 0 \\ -2a & < 0 \, \, \text{(bagi -2 dan tanda dibalik)} \\ a & > 0 \, \, ... \text{(HP}_1) \end{align*}$
$\clubsuit \, $ Karena $x_1 > 1 $ dan $x_2 < 1 $ , maka akarnya berbeda, syarat : $D > 0 $
$\begin{align*} D > 0 \rightarrow b^2-4ac & > 0 \\ (-a)^2 - 4 . 1 . [-(a+1)] & > 0 \\ a^2 + 4a + a & > 0 \\ (a+2)^2 & > 0 \, \, ... \text{(Terpenuhi untuk semua } \, a \in R) \\ \text{HP}_2 & = \{ a \in R , a \neq -2 \} \end{align*}$
Sehingga, HP = $\text{HP}_1 \cap \text{HP}_2 = \{ a > 0 \}$
Jadi, solusinya HP = $ \{ a > 0 \}. \heartsuit $
$x_1+x_2 = \frac{-b}{a} = \frac{-(-a)}{1} = a$
$x_1.x_2 = \frac{c}{a} = \frac{-(a+1)}{1} = -(a+1)$
$\clubsuit \, $ Memodifikasi dan dikalikan
$x_1 > 1 \Rightarrow x_1 - 1 > 0 \, \, \text{(positif)}$
$x_2 < 1 \Rightarrow x_2 - 1 < 0 \, \, \text{(negatif)}$
$\begin{align*} (x_1-1)(x_2-1) & < 0 \, \, \text{(positif kali negatif = negatif)}\\ x_1.x_2 - (x_1+x_2) + 1 & < 0 \\ -(a+1)-(a) + 1 & < 0 \\ -2a & < 0 \, \, \text{(bagi -2 dan tanda dibalik)} \\ a & > 0 \, \, ... \text{(HP}_1) \end{align*}$
$\clubsuit \, $ Karena $x_1 > 1 $ dan $x_2 < 1 $ , maka akarnya berbeda, syarat : $D > 0 $
$\begin{align*} D > 0 \rightarrow b^2-4ac & > 0 \\ (-a)^2 - 4 . 1 . [-(a+1)] & > 0 \\ a^2 + 4a + a & > 0 \\ (a+2)^2 & > 0 \, \, ... \text{(Terpenuhi untuk semua } \, a \in R) \\ \text{HP}_2 & = \{ a \in R , a \neq -2 \} \end{align*}$
Sehingga, HP = $\text{HP}_1 \cap \text{HP}_2 = \{ a > 0 \}$
Jadi, solusinya HP = $ \{ a > 0 \}. \heartsuit $
Nomor 4
Fungsi $f(x)=x^2+ax$ mempunyai grafik berikut

Grafik fungsi $g(x)=x^2-ax+5 $ adalah ...

Grafik fungsi $g(x)=x^2-ax+5 $ adalah ...
$\spadesuit \, $ Agar tidak rancu, alfabet $a$ diganti dengan $k$
$\spadesuit \, $ Analisa grafik $f(x) = x^2 + kx$

Kurva hadap atas, sehingga nilai $a > 0 $
Puncak di kanan sumbu Y, berlaku BeKa (Beda Kanan), artinya nilai $a$ dan $b$ harus beda. Karena $a > 0 $ , maka nilai $ b < 0 $ (beda) . Sehingga, $b < 0 \rightarrow k < 0 $ (nilai $k$ negatif) .
Catatan : Jika puncak di kiri sumbu Y, berlaku SaRi (Sama Kiri) .
$\spadesuit \, $ Analisa grafik $g(x) = x^2 - kx + 5$
Nilai $a = 1 > 0 \, $ artinya kurva hadap atas.
Nilai $b = -k > 0 \, $ ( $k$ negatif, sehingga nilai $-k \, $ positif).
Karena nilai $a$ dan $b$ sama (sama-sama positif), berlaku SaRi ( Sama Kiri), artinya puncak ada di sebelah kiri sumbu Y.
$c = 5$ , artinya kurva memotong sumbu Y di $y=5$ .
Sketsa grafik fungsi $ y = g(x) $
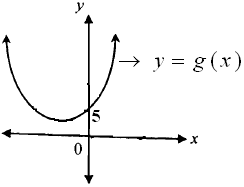
$\spadesuit \, $ Analisa grafik $f(x) = x^2 + kx$

Kurva hadap atas, sehingga nilai $a > 0 $
Puncak di kanan sumbu Y, berlaku BeKa (Beda Kanan), artinya nilai $a$ dan $b$ harus beda. Karena $a > 0 $ , maka nilai $ b < 0 $ (beda) . Sehingga, $b < 0 \rightarrow k < 0 $ (nilai $k$ negatif) .
Catatan : Jika puncak di kiri sumbu Y, berlaku SaRi (Sama Kiri) .
$\spadesuit \, $ Analisa grafik $g(x) = x^2 - kx + 5$
Nilai $a = 1 > 0 \, $ artinya kurva hadap atas.
Nilai $b = -k > 0 \, $ ( $k$ negatif, sehingga nilai $-k \, $ positif).
Karena nilai $a$ dan $b$ sama (sama-sama positif), berlaku SaRi ( Sama Kiri), artinya puncak ada di sebelah kiri sumbu Y.
$c = 5$ , artinya kurva memotong sumbu Y di $y=5$ .
Sketsa grafik fungsi $ y = g(x) $

Nomor 5
Nilai $x$ yang memenuhi pertidaksamaan $\frac{x+1}{x+1} > \frac{x}{x-1} $ adalah ...
$\clubsuit \, $ Mengelompokkan ke ruas kiri
$\begin{align*} \frac{x+1}{x+1} & > \frac{x}{x-1} \\ \frac{x+1}{x+1} - \frac{x}{x-1} & > 0 \\ \frac{(x+1)(x-1) - x(x+1)}{(x+1)(x-1)} & > 0 \\ \frac{-(x+1)}{(x+1)(x-1)} & > 0 \\ x= -1 \, & \vee \, x = 1 \end{align*}$

Jadi, HP = $ \{ x < -1 \vee -1 < x < 1 \}. \heartsuit$
$\begin{align*} \frac{x+1}{x+1} & > \frac{x}{x-1} \\ \frac{x+1}{x+1} - \frac{x}{x-1} & > 0 \\ \frac{(x+1)(x-1) - x(x+1)}{(x+1)(x-1)} & > 0 \\ \frac{-(x+1)}{(x+1)(x-1)} & > 0 \\ x= -1 \, & \vee \, x = 1 \end{align*}$

Jadi, HP = $ \{ x < -1 \vee -1 < x < 1 \}. \heartsuit$
Cara II
$\clubsuit \, \frac{x+1}{x+1} = 1 \, $ , dengan syarat : $x \neq -1 $
Sehingga , HP$_1 = \{ x \neq -1 \} $ .
$\clubsuit \, $ Mengelompokkan ke ruas kiri
$\begin{align*} \frac{x+1}{x+1} & > \frac{x}{x-1} \\ 1 - \frac{x}{x-1} & > 0 \\ \frac{(x-1) - x}{(x-1)} & > 0 \\ \frac{-1}{(x-1)} & > 0 \\ x & = 1 \end{align*}$

HP$_2 = \{ x < 1 \} $ .
Sehingga, HP = $\text{HP}_1 \cap \text{HP}_2 = \{ x < -1 \vee -1 < x < 1 \}$
Jadi, HP = $ \{ x < -1 \vee -1 < x < 1 \}. \heartsuit$
$\clubsuit \, \frac{x+1}{x+1} = 1 \, $ , dengan syarat : $x \neq -1 $
Sehingga , HP$_1 = \{ x \neq -1 \} $ .
$\clubsuit \, $ Mengelompokkan ke ruas kiri
$\begin{align*} \frac{x+1}{x+1} & > \frac{x}{x-1} \\ 1 - \frac{x}{x-1} & > 0 \\ \frac{(x-1) - x}{(x-1)} & > 0 \\ \frac{-1}{(x-1)} & > 0 \\ x & = 1 \end{align*}$

HP$_2 = \{ x < 1 \} $ .
Sehingga, HP = $\text{HP}_1 \cap \text{HP}_2 = \{ x < -1 \vee -1 < x < 1 \}$
Jadi, HP = $ \{ x < -1 \vee -1 < x < 1 \}. \heartsuit$
Cara III : Metode Suka (substitusi angka)
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
yang ada $x=1$ dan $x=-1$ salah karena penyebutnya akan nol, opsi yang salah adalah A, B, dan C.
$\begin{align*} \text{Pilih} \, x=0 \Rightarrow \frac{x+1}{x+1} & > \frac{x}{x-1} \\ \frac{0+1}{0+1} & > \frac{0}{0-1} \\ 1 & > 0 \, \, \text{(benar)} \end{align*}$
yang ada $x=0$ benar, opsi yang salah adalah D.
Jadi, opsi yang benar adalah E yaitu HP = $ \{ x < -1 \vee -1 < x < 1 \}. \heartsuit$
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
yang ada $x=1$ dan $x=-1$ salah karena penyebutnya akan nol, opsi yang salah adalah A, B, dan C.
$\begin{align*} \text{Pilih} \, x=0 \Rightarrow \frac{x+1}{x+1} & > \frac{x}{x-1} \\ \frac{0+1}{0+1} & > \frac{0}{0-1} \\ 1 & > 0 \, \, \text{(benar)} \end{align*}$
yang ada $x=0$ benar, opsi yang salah adalah D.
Jadi, opsi yang benar adalah E yaitu HP = $ \{ x < -1 \vee -1 < x < 1 \}. \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.