Nomor 1
Diketahui vektor $\vec{u}=(a, -2, -1) $ dan $\vec{v}=(a, a, -1) $ . Jika vektor $\vec{u} $ tegak lurus pada $\vec{v}$ ,
maka nilai $a$ adalah ...
$\clubsuit \, $ vektor $ \vec{u} $ tegak lurus vektor $ \vec{v} $ , syarat : $\vec{u}.\vec{v} = 0 $
$\begin{align*} \vec{u} . \vec{v} & = 0 \\ \, \, \, a.a+(-2).a+(-1).(-1) & = 0 \\ a^2-2a+1 & = 0 \\ (a-1)^2 & = 0 \\ a-1 & = 0 \\ a & = 1 \end{align*}$
Jadi, nilai $ a = 1 . \heartsuit $
$\begin{align*} \vec{u} . \vec{v} & = 0 \\ \, \, \, a.a+(-2).a+(-1).(-1) & = 0 \\ a^2-2a+1 & = 0 \\ (a-1)^2 & = 0 \\ a-1 & = 0 \\ a & = 1 \end{align*}$
Jadi, nilai $ a = 1 . \heartsuit $
Nomor 2
Pernyataan berikut yang benar adalah ...
(A) Jika $\sin x = \sin y $ , maka $x=y$
(B) Untuk setiap vektor $\vec{u}, \vec{v} $ dan $\vec{w} $ berlaku $\vec{u}.(\vec{v}.\vec{w}) = (\vec{u}.\vec{v}).\vec{w} $
(C) Jika $\int \limits_a^b f(x)dx=0 $ , maka $f(x) = 0 $
(D) Ada fungsi $f$ sehingga $\displaystyle \lim_{x \to c} f(x) \neq f(c) $ untuk suatu $c$
(E) $1-\cos 2x = 2\cos ^2 x $
(A) Jika $\sin x = \sin y $ , maka $x=y$
(B) Untuk setiap vektor $\vec{u}, \vec{v} $ dan $\vec{w} $ berlaku $\vec{u}.(\vec{v}.\vec{w}) = (\vec{u}.\vec{v}).\vec{w} $
(C) Jika $\int \limits_a^b f(x)dx=0 $ , maka $f(x) = 0 $
(D) Ada fungsi $f$ sehingga $\displaystyle \lim_{x \to c} f(x) \neq f(c) $ untuk suatu $c$
(E) $1-\cos 2x = 2\cos ^2 x $
$\spadesuit \, $ Analisa setiap pilihan :
(A) Jika $\sin x = \sin y $ , maka belum tentu $x=y$ ,
contohnya $\sin 30^o = \sin 150^o $ maka $30^o \neq 150^o $ . (salah)
(B) Perkalian dot hasilnya skalar (bilangan), dan perkalian dot hanya berlaku vektor dengan vektor bukan dengan skalar.
$\vec{u}.(\vec{v}.\vec{w}) = \vec{u} $ . (skalar)
tidak bisa dioperasikan (salah)
(C) Ada fungsi lain dengan $f(x) \neq 0 $ yang menyebabkan $\int \limits_a^b f(x)dx=0 $ .
Contoh : $f(x) = x $
$\int \limits_{-1}^1 f(x)dx = \int \limits_{-1}^1 x dx = \left[ \frac{1}{2} x^2 \right]_{-1}^1 = 0 $
(D) $\displaystyle \lim_{x \to c} f(x) \neq f(c) $ artinya fungsi diskontinu, dan fungsi tersebut ada.
Contoh : $f(x) = \frac{1}{x-1} $ diskontinu saat $x=1 $ . (Benar)
(E) konsep dasar :
$\cos 2x = \cos ^2 x - \sin ^2 x $ dan $ 1- \cos ^2 x = \sin ^2 x $ (identitas)
$\begin{align*} 1- \cos 2x & = 1- ( \cos ^2 x - \sin ^2 x ) \\ & = (1- \cos ^2 x ) + \sin ^2 x \\ & = \sin ^2 x + \sin ^2 x \\ 1- \cos 2x & = 2\sin ^2 x \end{align*}$
Artinya $ 1- \cos 2x \neq 2\cos ^2 x $ . (salah)
Jadi, yang benar adalah opsi D. $ \heartsuit $
(A) Jika $\sin x = \sin y $ , maka belum tentu $x=y$ ,
contohnya $\sin 30^o = \sin 150^o $ maka $30^o \neq 150^o $ . (salah)
(B) Perkalian dot hasilnya skalar (bilangan), dan perkalian dot hanya berlaku vektor dengan vektor bukan dengan skalar.
$\vec{u}.(\vec{v}.\vec{w}) = \vec{u} $ . (skalar)
tidak bisa dioperasikan (salah)
(C) Ada fungsi lain dengan $f(x) \neq 0 $ yang menyebabkan $\int \limits_a^b f(x)dx=0 $ .
Contoh : $f(x) = x $
$\int \limits_{-1}^1 f(x)dx = \int \limits_{-1}^1 x dx = \left[ \frac{1}{2} x^2 \right]_{-1}^1 = 0 $
(D) $\displaystyle \lim_{x \to c} f(x) \neq f(c) $ artinya fungsi diskontinu, dan fungsi tersebut ada.
Contoh : $f(x) = \frac{1}{x-1} $ diskontinu saat $x=1 $ . (Benar)
(E) konsep dasar :
$\cos 2x = \cos ^2 x - \sin ^2 x $ dan $ 1- \cos ^2 x = \sin ^2 x $ (identitas)
$\begin{align*} 1- \cos 2x & = 1- ( \cos ^2 x - \sin ^2 x ) \\ & = (1- \cos ^2 x ) + \sin ^2 x \\ & = \sin ^2 x + \sin ^2 x \\ 1- \cos 2x & = 2\sin ^2 x \end{align*}$
Artinya $ 1- \cos 2x \neq 2\cos ^2 x $ . (salah)
Jadi, yang benar adalah opsi D. $ \heartsuit $
Nomor 3
Luas daerah di bawah $y=-x^2+8x$ , di atas $y=6x-24 $ , dan terletak di kuadran I adalah ...
$\clubsuit \, $ gambarnya :
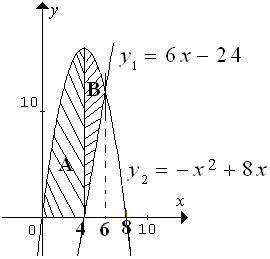
Luas daerah yang dimaksud adalah daerah A dan B.
$\clubsuit \, $ Titik potong kedua kurva
$\begin{align*} y_1 & = y_2 \\ 6x-24 & = -x^2+8x \\ x^2 -2x -24 & = 0 \\ (x+4)(x-6) & = 0 \\ x=-4 & \vee x = 6 \end{align*}$
$\clubsuit \, $ Menentukan luas
$\begin{align*} \text{Luas} & = \text{Luas A} \, + \, \text{Luas B} \\ & = \int \limits_{0}^4 y_2 dx + \int \limits_{4}^6 (y_2-y_1) dx \\ & = \int \limits_{0}^4 (-x^2+8x) dx + \int \limits_{4}^6 (-x^2+8x)-(6x-24) dx \\ & = \int \limits_{0}^4 (-x^2+8x) dx + \int \limits_{4}^6 (-x^2+2x+24) dx \end{align*}$
Jadi, luasnya adalah $ \int \limits_{0}^4 -x^2+8x) dx + \int \limits_{4}^6 (-x^2+2x+24) dx . \heartsuit $

Luas daerah yang dimaksud adalah daerah A dan B.
$\clubsuit \, $ Titik potong kedua kurva
$\begin{align*} y_1 & = y_2 \\ 6x-24 & = -x^2+8x \\ x^2 -2x -24 & = 0 \\ (x+4)(x-6) & = 0 \\ x=-4 & \vee x = 6 \end{align*}$
$\clubsuit \, $ Menentukan luas
$\begin{align*} \text{Luas} & = \text{Luas A} \, + \, \text{Luas B} \\ & = \int \limits_{0}^4 y_2 dx + \int \limits_{4}^6 (y_2-y_1) dx \\ & = \int \limits_{0}^4 (-x^2+8x) dx + \int \limits_{4}^6 (-x^2+8x)-(6x-24) dx \\ & = \int \limits_{0}^4 (-x^2+8x) dx + \int \limits_{4}^6 (-x^2+2x+24) dx \end{align*}$
Jadi, luasnya adalah $ \int \limits_{0}^4 -x^2+8x) dx + \int \limits_{4}^6 (-x^2+2x+24) dx . \heartsuit $
Nomor 4
Delapan titik terletak pada bidang datar sehingga tidak ada tiga titik yang segaris. Banyak segitiga yang dapa dibuat
dengan titik-titik sudut dari titik-titik tersebut adalah ...
$\spadesuit \, $ Untuk membuat segitiga dibutuhkan 3 titik , artinya akan dipilih 3 titik dari 8 titik yang ada
tanpa memperhatikan urutan ($\Delta$ABC sama saja dengan $\Delta$BCA ) sehingga menggunakan kombinasi.
Total cara = $C_3^8 = 56 $ cara.
Jadi, banyak segitiga yang terbentuk ada 56 segitiga. $ \heartsuit $
Total cara = $C_3^8 = 56 $ cara.
Jadi, banyak segitiga yang terbentuk ada 56 segitiga. $ \heartsuit $
Nomor 5
Vektor $\vec{u} = 4\vec{i} + b\vec{j}+c\vec{k} $ tegak lurus vektor $\vec{w} = 2\vec{i} -2\vec{j}+3\vec{k} $ dan
$|\vec{u} | = 2|\vec{w}| $ , maka nilai $b$ memenuhi ...
$\vec{u} = (4, \, \, b, \, \, c ) $ , $\vec{w} = (2, \, \, -2, \, \, 3) $
panjang vektor $\vec{u} $ : $|\vec{u}| = \sqrt{4^2+b^2+c^2} = \sqrt{16+b^2+c^2} $
panjang vektor $\vec{w} $ : $|\vec{w}| = \sqrt{2^2+(-2)^2+3^2} = \sqrt{17} $
$\clubsuit \, $ Vektor $\vec{u} $ dan $\vec{w} $ tegak lurus, syarat : $\vec{u}. \vec{w} = 0 $
$\begin{align} \vec{u}. \vec{w} & = 0 \\ 4.2 + b.(-2)+c.3 & = 0 \\ 8-2b+3c & = 0 \\ c & = \frac{2b-8}{3} \, \, \, \text{...pers(i)} \end{align}$
$\clubsuit \, $ Menentukan bentuk $b$ dengan substitusi pers(i)
$\begin{align} |\vec{u} | & = 2|\vec{w}| \\ \sqrt{16+b^2+c^2} & = 2 \sqrt{17} \, \, \, \text{(dikuadratkan)} \\ 16+b^2+c^2 & = 4 \times 17 \, \, \, \text{...pers(i)} \\ 16+b^2+\left( \frac{2b-8}{3} \right)^2 & = 68 \\ b^2+\left( \frac{4b^2-32b+64}{9} \right)^2 & = 52 \, \, \, \text{(kali 9)} \\ 9b^2+ 4b^2-32b+64 & = 468 \\ 13b^2 -32b - 404 & = 0 \end{align}$
Jadi, nilai $b$ memenuhi $ 13b^2 -32b - 404 = 0. \heartsuit$
panjang vektor $\vec{u} $ : $|\vec{u}| = \sqrt{4^2+b^2+c^2} = \sqrt{16+b^2+c^2} $
panjang vektor $\vec{w} $ : $|\vec{w}| = \sqrt{2^2+(-2)^2+3^2} = \sqrt{17} $
$\clubsuit \, $ Vektor $\vec{u} $ dan $\vec{w} $ tegak lurus, syarat : $\vec{u}. \vec{w} = 0 $
$\begin{align} \vec{u}. \vec{w} & = 0 \\ 4.2 + b.(-2)+c.3 & = 0 \\ 8-2b+3c & = 0 \\ c & = \frac{2b-8}{3} \, \, \, \text{...pers(i)} \end{align}$
$\clubsuit \, $ Menentukan bentuk $b$ dengan substitusi pers(i)
$\begin{align} |\vec{u} | & = 2|\vec{w}| \\ \sqrt{16+b^2+c^2} & = 2 \sqrt{17} \, \, \, \text{(dikuadratkan)} \\ 16+b^2+c^2 & = 4 \times 17 \, \, \, \text{...pers(i)} \\ 16+b^2+\left( \frac{2b-8}{3} \right)^2 & = 68 \\ b^2+\left( \frac{4b^2-32b+64}{9} \right)^2 & = 52 \, \, \, \text{(kali 9)} \\ 9b^2+ 4b^2-32b+64 & = 468 \\ 13b^2 -32b - 404 & = 0 \end{align}$
Jadi, nilai $b$ memenuhi $ 13b^2 -32b - 404 = 0. \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.