Nomor 1
Nilai $p$ agar vektor $\, \, pi+2j-6k \, \, $ dan $\, \, 4i-3j+k \, \, $ saling tegak lurus adalah ...
$\clubsuit \, $ Misalkan vektor-vektornya
$\vec{u} = (p \, \, \, 2 \, \, \, -6) $ dan $\vec{v} = (4 \, \, \, -3 \, \, \, 1) $
$\clubsuit \, $ Vektor $\vec{u} $ tegak lurus vekor $\vec{v}$ , syarat : $\vec{u}.\vec{v} = 0 $
$\begin{align*} \vec{u}.\vec{v} & = 0 \\ \, \, \, p.4 + 2.(-3) + (-6).1 & = 0 \\ 4p-6-6 & = 0 \\ 4p & = 12 \\ p & = 3 \end{align*}$
Jadi, nilai $p=3 .\heartsuit $
$\vec{u} = (p \, \, \, 2 \, \, \, -6) $ dan $\vec{v} = (4 \, \, \, -3 \, \, \, 1) $
$\clubsuit \, $ Vektor $\vec{u} $ tegak lurus vekor $\vec{v}$ , syarat : $\vec{u}.\vec{v} = 0 $
$\begin{align*} \vec{u}.\vec{v} & = 0 \\ \, \, \, p.4 + 2.(-3) + (-6).1 & = 0 \\ 4p-6-6 & = 0 \\ 4p & = 12 \\ p & = 3 \end{align*}$
Jadi, nilai $p=3 .\heartsuit $
Nomor 2
Jika garis singgung kurva $y=2x\cos 3x $ di titik ($\pi , -2\pi $ ) tegak lurus dengan garis $g$ , maka persamaan
garis $g$ adalah ...
$\spadesuit \, $ Gradien garis singgung di titik ($\pi , -2\pi $ ), $m = f^\prime (\pi ) $
$\begin{align} y & =2x\cos 3x \\ y^\prime & = 2\cos 3x - 6x\sin 3x \\ m_1 & = f^\prime (\pi ) \\ m_1 & = 2\cos 3\pi - 6\pi . \sin 3\pi \\ & = 2.(-1) - 6\pi . (0) \\ m_1 & = -2 \end{align}$
$\spadesuit \, $ Garis $g$ tegak lurus garis singgung, sehingga gradiennya
$m_1.m_2 = -1 \rightarrow m_2 = \frac{-1}{m_1} = \frac{-1}{-2} = \frac{1}{2} $
sehingga gradien garis $g$ adalah $m = \frac{1}{2} $
$\spadesuit \, $ Persamaan garis $g$
$\begin{align} y-y_1 & = m(x-x_1) \\ y-(-2\pi) & = \frac{1}{2} (x- \pi) \, \, \, \text{(kali 2)} \\ 2y + 4\pi & = (x- \pi) \\ y & = \frac{1}{2}x - \frac{5}{2}\pi \end{align}$
Jadi, persamaan garis $g$ adalah $ y = \frac{1}{2}x - \frac{5}{2}\pi . \heartsuit $
$\begin{align} y & =2x\cos 3x \\ y^\prime & = 2\cos 3x - 6x\sin 3x \\ m_1 & = f^\prime (\pi ) \\ m_1 & = 2\cos 3\pi - 6\pi . \sin 3\pi \\ & = 2.(-1) - 6\pi . (0) \\ m_1 & = -2 \end{align}$
$\spadesuit \, $ Garis $g$ tegak lurus garis singgung, sehingga gradiennya
$m_1.m_2 = -1 \rightarrow m_2 = \frac{-1}{m_1} = \frac{-1}{-2} = \frac{1}{2} $
sehingga gradien garis $g$ adalah $m = \frac{1}{2} $
$\spadesuit \, $ Persamaan garis $g$
$\begin{align} y-y_1 & = m(x-x_1) \\ y-(-2\pi) & = \frac{1}{2} (x- \pi) \, \, \, \text{(kali 2)} \\ 2y + 4\pi & = (x- \pi) \\ y & = \frac{1}{2}x - \frac{5}{2}\pi \end{align}$
Jadi, persamaan garis $g$ adalah $ y = \frac{1}{2}x - \frac{5}{2}\pi . \heartsuit $
Nomor 3
Diketahui suku banyak $P(x) = x^4+2x^3-9x^2-2x+k $ habis dibagi $x-2 $ . Jika $P(x) $ dibagi $x-1 $ sisanya adalah ...
$\clubsuit \, $ Teorema sisa : $\frac{P(x)}{x-a} \rightarrow $ Sisa = $P(a)$
$\clubsuit \, P(x) $ habis dibagi $x-2$ , maka sisanya nol
$\begin{align} P(2) & = \text{sisa} \\ 2^4+2.2^3-9.2^2-2.2+k & = 0 \\ -8 + k & = 0 \\ k & = 8 \end{align}$
Sehingga $P(x) = x^4+2x^3-9x^2-2x+8 $
$\spadesuit \, P(x) $ dibagi $x-1 \rightarrow $ sisa = $P(1)$
Sisa = $p(1) = 1^4+2.1^3-9.1^2-2.1+8 = 0 $
Jadi, sisanya adalah 0 . $ \heartsuit $
$\clubsuit \, P(x) $ habis dibagi $x-2$ , maka sisanya nol
$\begin{align} P(2) & = \text{sisa} \\ 2^4+2.2^3-9.2^2-2.2+k & = 0 \\ -8 + k & = 0 \\ k & = 8 \end{align}$
Sehingga $P(x) = x^4+2x^3-9x^2-2x+8 $
$\spadesuit \, P(x) $ dibagi $x-1 \rightarrow $ sisa = $P(1)$
Sisa = $p(1) = 1^4+2.1^3-9.1^2-2.1+8 = 0 $
Jadi, sisanya adalah 0 . $ \heartsuit $
Nomor 4
Persamaan kuadrat yang mempunyai akar $a$ dan $b$ sehingga $\frac{1}{a}+\frac{1}{b} = \frac{7}{10} $ adalah ...
$\spadesuit \, $ Menyederhanakan soal
$\begin{align} \frac{1}{a}+\frac{1}{b} & = \frac{7}{10} \\ \frac{a+b}{ab} & = \frac{7}{10} \\ \frac{a+b}{ab} & = \frac{7}{10} = \frac{14}{20} = \frac{21}{30} = \frac{28}{40} = .... \end{align}$
artinya nilai terkecil dari $a+b = 7 $ dan $ab=10$
$\spadesuit \, $ Persamaan kuadrat yang akar-akarnya $a$ dan $b$
$\begin{align} x^2 - (a+b)x+ab & = 0 \\ x^2 - 7x+ 10 & = 0 \end{align}$
Jadi, persamaan kuadratnya adalah $ x^2 - 7x+ 10 = 0 . \heartsuit $
$\begin{align} \frac{1}{a}+\frac{1}{b} & = \frac{7}{10} \\ \frac{a+b}{ab} & = \frac{7}{10} \\ \frac{a+b}{ab} & = \frac{7}{10} = \frac{14}{20} = \frac{21}{30} = \frac{28}{40} = .... \end{align}$
artinya nilai terkecil dari $a+b = 7 $ dan $ab=10$
$\spadesuit \, $ Persamaan kuadrat yang akar-akarnya $a$ dan $b$
$\begin{align} x^2 - (a+b)x+ab & = 0 \\ x^2 - 7x+ 10 & = 0 \end{align}$
Jadi, persamaan kuadratnya adalah $ x^2 - 7x+ 10 = 0 . \heartsuit $
Nomor 5
Diketahui limas beraturan T.ABCD dengan panjang rusuk 6 cm. Titik P pada CT sehingga TP : PC = 2 : 1. Jarak P ke bidang
BDT adalah ...
$\clubsuit \, $ Gambarnya :
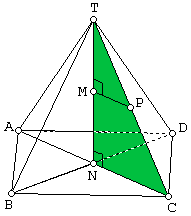

$\clubsuit \, $ Jarak P ke bidang BDT sama dengan jarak Pke garis TN atau panjang PM
$\clubsuit \, $ Konsep kesebangunan, $\Delta$TPM sebangun dengan $\Delta$TCN
$\begin{align} \frac{PM}{NC} & = \frac{TP}{TC} \\ \frac{PM}{3\sqrt{2}} & = \frac{4}{6} \\ PM & = \frac{4}{6} . 3\sqrt{2} \\ PM & = 2\sqrt{2} \end{align}$
Jadi, jaraknya adalah $ 2\sqrt{2} . \heartsuit$


$\clubsuit \, $ Jarak P ke bidang BDT sama dengan jarak Pke garis TN atau panjang PM
$\clubsuit \, $ Konsep kesebangunan, $\Delta$TPM sebangun dengan $\Delta$TCN
$\begin{align} \frac{PM}{NC} & = \frac{TP}{TC} \\ \frac{PM}{3\sqrt{2}} & = \frac{4}{6} \\ PM & = \frac{4}{6} . 3\sqrt{2} \\ PM & = 2\sqrt{2} \end{align}$
Jadi, jaraknya adalah $ 2\sqrt{2} . \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.