Nomor 6
Himpunan penyelesaian pertidaksamaan $\frac{2-\sin \theta}{\cos \theta} \leq \frac{\cos \theta}{\sin \theta} $ untuk
$0 \leq \theta \leq \frac{\pi}{2} $ adalah ...
$\spadesuit \, $ Ruas kanan di nol kan
$\begin{align} \frac{2-\sin \theta}{\cos \theta} & \leq \frac{\cos \theta}{\sin \theta} \\ \frac{2-\sin \theta}{\cos \theta} - \frac{\cos \theta}{\sin \theta}& \leq 0 \\ \frac{2\sin \theta - \sin ^2 \theta - \cos ^2 \theta}{\cos \theta \sin \theta}& \leq 0 \\ \frac{2\sin \theta - ( \sin ^2 \theta + \cos ^2 \theta ) }{\cos \theta \sin \theta}& \leq 0 \\ \frac{2\sin \theta - 1 }{\cos \theta \sin \theta}& \leq 0 \end{align}$
$\spadesuit \, $ Menentukan nilai $\theta$
$2\sin \theta - 1 \rightarrow \sin \theta = \frac{1}{2} \rightarrow \theta = \frac{\pi}{6} , \frac{5\pi}{6} $
$ \cos \theta = 0 \rightarrow \theta = \frac{\pi}{2} , \frac{3\pi}{2} $
$\sin \theta = 0 \rightarrow \theta = 0 , \pi $

$\spadesuit \, $ Karena $\theta$ pada interval $0 \leq \theta \leq \frac{\pi}{2} $ , maka solusi yang memenuhi adalah $0 < \theta \leq \frac{\pi}{6} $
Jadi, HP = $ 0 < \theta \leq \frac{\pi}{6} . \heartsuit $
$\begin{align} \frac{2-\sin \theta}{\cos \theta} & \leq \frac{\cos \theta}{\sin \theta} \\ \frac{2-\sin \theta}{\cos \theta} - \frac{\cos \theta}{\sin \theta}& \leq 0 \\ \frac{2\sin \theta - \sin ^2 \theta - \cos ^2 \theta}{\cos \theta \sin \theta}& \leq 0 \\ \frac{2\sin \theta - ( \sin ^2 \theta + \cos ^2 \theta ) }{\cos \theta \sin \theta}& \leq 0 \\ \frac{2\sin \theta - 1 }{\cos \theta \sin \theta}& \leq 0 \end{align}$
$\spadesuit \, $ Menentukan nilai $\theta$
$2\sin \theta - 1 \rightarrow \sin \theta = \frac{1}{2} \rightarrow \theta = \frac{\pi}{6} , \frac{5\pi}{6} $
$ \cos \theta = 0 \rightarrow \theta = \frac{\pi}{2} , \frac{3\pi}{2} $
$\sin \theta = 0 \rightarrow \theta = 0 , \pi $

$\spadesuit \, $ Karena $\theta$ pada interval $0 \leq \theta \leq \frac{\pi}{2} $ , maka solusi yang memenuhi adalah $0 < \theta \leq \frac{\pi}{6} $
Jadi, HP = $ 0 < \theta \leq \frac{\pi}{6} . \heartsuit $
Nomor 7
Panjang dua sisi suatu segitiga adalah 10 cm dan 8 cm. Semua nilai berikut dapat menjadi nilai keliling segitiga tersebut, kecuali ...
$\clubsuit \, $ Pertidaksamaan pada sisi segitiga
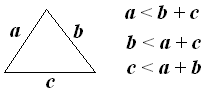
$\clubsuit \, $ Deskripsi gambar

artinya nilai $x$ terbesar adalah kurang dari 18 .
$\clubsuit \, $ Keliling segitiga
$\begin{align} \text{Keliling} \, \Delta & = 10 + 8 + x \\ \text{Keliling} \, \Delta & < 10 + 8 + 18 \\ \text{Keliling} \, \Delta & < 36 \end{align}$
sehingga keliling yang mungkin kurang dari 36.
Jadi, keliling yang tidak mungkin lebih besar sama dengan 36, yaitu opsi E. $ \heartsuit$
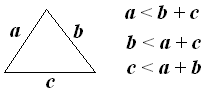
$\clubsuit \, $ Deskripsi gambar

artinya nilai $x$ terbesar adalah kurang dari 18 .
$\clubsuit \, $ Keliling segitiga
$\begin{align} \text{Keliling} \, \Delta & = 10 + 8 + x \\ \text{Keliling} \, \Delta & < 10 + 8 + 18 \\ \text{Keliling} \, \Delta & < 36 \end{align}$
sehingga keliling yang mungkin kurang dari 36.
Jadi, keliling yang tidak mungkin lebih besar sama dengan 36, yaitu opsi E. $ \heartsuit$
Cara II
$\clubsuit \, $ Jika diketahui dua sisi pada segitiga , misalkan $a$ dan $b$ dengan $a \geq b $ , maka rentang keliling segitiga yang mungkin adalah $2a < K \Delta < 2(a+b) $
$\clubsuit \, $ diketahui panjang sisi segitiga, $a=10$ , dan $b=8$ , Rentang kelilingnya :
$\begin{align} 2a < & \text{Keliling} \, \Delta < 2 (a+b) \\ 2.10 < & \text{Keliling} \, \Delta < 2 (10+8) \\ 20 < & \text{Keliling} \, \Delta < 36 \end{align}$
Jadi, keliling yang tidak mungkin diluar interval di atas, yaitu 36, opsi E. $ \heartsuit$
$\clubsuit \, $ Jika diketahui dua sisi pada segitiga , misalkan $a$ dan $b$ dengan $a \geq b $ , maka rentang keliling segitiga yang mungkin adalah $2a < K \Delta < 2(a+b) $
$\clubsuit \, $ diketahui panjang sisi segitiga, $a=10$ , dan $b=8$ , Rentang kelilingnya :
$\begin{align} 2a < & \text{Keliling} \, \Delta < 2 (a+b) \\ 2.10 < & \text{Keliling} \, \Delta < 2 (10+8) \\ 20 < & \text{Keliling} \, \Delta < 36 \end{align}$
Jadi, keliling yang tidak mungkin diluar interval di atas, yaitu 36, opsi E. $ \heartsuit$
Nomor 8
Diketahui fungsi $g$ kontinu di $ x = 3 $ dan $\displaystyle \lim_{x \to 3} g(x) = 2 $ .
Nilai $\displaystyle \lim_{x \to 3} \left( g(x)\frac{x-3}{\sqrt{x}-\sqrt{3}} \right) $ adalah ...
Nilai $\displaystyle \lim_{x \to 3} \left( g(x)\frac{x-3}{\sqrt{x}-\sqrt{3}} \right) $ adalah ...
$\spadesuit \, $ Konsep dasar :
$\displaystyle \lim_{x \to a} f(x).g(x) = \displaystyle \lim_{x \to a} f(x) . \displaystyle \lim_{x \to a} g(x)$ .
$\spadesuit \, $ Menyederhanakan limitnya
$\begin{align*} \displaystyle \lim_{x \to 3} \left( g(x)\frac{x-3}{\sqrt{x}-\sqrt{3}} \right) & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{x-3}{\sqrt{x}-\sqrt{3}} \, \, \, \text{(rasionalkan)} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{x-3}{\sqrt{x}-\sqrt{3}} . \frac{\sqrt{x}+\sqrt{3}}{\sqrt{x}+\sqrt{3}} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{(x-3)(\sqrt{x}+\sqrt{3})}{(x-3)} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} (\sqrt{x}+\sqrt{3}) \\ & = 2 \times (\sqrt{3} + \sqrt{3}) \\ & = 2 \times 2\sqrt{3} \\ & = 4\sqrt{3} \end{align*}$
Jadi, hasilnya adalah $ 4\sqrt{3} . \heartsuit$
$\spadesuit \, $ Menyederhanakan limitnya
$\begin{align*} \displaystyle \lim_{x \to 3} \left( g(x)\frac{x-3}{\sqrt{x}-\sqrt{3}} \right) & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{x-3}{\sqrt{x}-\sqrt{3}} \, \, \, \text{(rasionalkan)} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{x-3}{\sqrt{x}-\sqrt{3}} . \frac{\sqrt{x}+\sqrt{3}}{\sqrt{x}+\sqrt{3}} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{(x-3)(\sqrt{x}+\sqrt{3})}{(x-3)} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} (\sqrt{x}+\sqrt{3}) \\ & = 2 \times (\sqrt{3} + \sqrt{3}) \\ & = 2 \times 2\sqrt{3} \\ & = 4\sqrt{3} \end{align*}$
Jadi, hasilnya adalah $ 4\sqrt{3} . \heartsuit$
Cara II
$\spadesuit \, $ Konsep dasar : $\displaystyle \lim_{x \to a} f(x).g(x) = \displaystyle \lim_{x \to a} f(x) . \displaystyle \lim_{x \to a} g(x)$ .
$\spadesuit \, $ Menyederhanakan limitnya
$\begin{align*} \displaystyle \lim_{x \to 3} \left( g(x)\frac{x-3}{\sqrt{x}-\sqrt{3}} \right) & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{x-3}{\sqrt{x}-\sqrt{3}} \, \, \, \text{(turunan)} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{1}{\frac{1}{2\sqrt{x}}} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} 2\sqrt{x} \\ & = 2 \times 2\sqrt{3} \\ & = 4\sqrt{3} \end{align*}$
Jadi, hasilnya adalah $ 4\sqrt{3} . \heartsuit$
$\spadesuit \, $ Konsep dasar : $\displaystyle \lim_{x \to a} f(x).g(x) = \displaystyle \lim_{x \to a} f(x) . \displaystyle \lim_{x \to a} g(x)$ .
$\spadesuit \, $ Menyederhanakan limitnya
$\begin{align*} \displaystyle \lim_{x \to 3} \left( g(x)\frac{x-3}{\sqrt{x}-\sqrt{3}} \right) & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{x-3}{\sqrt{x}-\sqrt{3}} \, \, \, \text{(turunan)} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} \frac{1}{\frac{1}{2\sqrt{x}}} \\ & = \displaystyle \lim_{x \to 3} g(x). \displaystyle \lim_{x \to 3} 2\sqrt{x} \\ & = 2 \times 2\sqrt{3} \\ & = 4\sqrt{3} \end{align*}$
Jadi, hasilnya adalah $ 4\sqrt{3} . \heartsuit$
Nomor 9
Diketahui fungsi $f$ dan $g$ dengan $g(x)=f(x^2+2) $ . Jika diketahui bahwa $g^\prime (1) = 8 $ , maka nilai
$f^\prime (3) $ adalah ...
$\clubsuit \, $ Konsep dasar
$y=f\left[ h(x) \right] \rightarrow y^\prime = f^\prime \left[ h(x) \right] . h^\prime (x) $
$\clubsuit \, $ Menurunkan fungsinya dan substitusi $x=1$
$\begin{align*} g(x) & =f(x^2+2) \\ g^\prime (x) & = f^\prime (x^2+2) . (2x) \\ x=1 \rightarrow g^\prime (1) & = f^\prime (1^2+2) . (2.1) \\ 8 & = f^\prime (3) . 2 \\ f^\prime (3) & = \frac{8}{2} \\ f^\prime (3) & = 4 \end{align*}$
Jadi, nilai $ f^\prime (3) = 4 . \heartsuit $
$y=f\left[ h(x) \right] \rightarrow y^\prime = f^\prime \left[ h(x) \right] . h^\prime (x) $
$\clubsuit \, $ Menurunkan fungsinya dan substitusi $x=1$
$\begin{align*} g(x) & =f(x^2+2) \\ g^\prime (x) & = f^\prime (x^2+2) . (2x) \\ x=1 \rightarrow g^\prime (1) & = f^\prime (1^2+2) . (2.1) \\ 8 & = f^\prime (3) . 2 \\ f^\prime (3) & = \frac{8}{2} \\ f^\prime (3) & = 4 \end{align*}$
Jadi, nilai $ f^\prime (3) = 4 . \heartsuit $
Nomor 10
Daerah R di kuadran satu, dibatasi oleh grafik $y=x^2, \, y=x+2 $ dan $y=0 $ . Integral yang menyatakan luas daerah R adalah ...
$\spadesuit \, $ Gambarnya

$\spadesuit \, $ Titik potong kedua kurva
$\begin{align*} y_1 & = y_2 \\ x^2 & = x + 2 \\ x^2 - x- 2 & = 0 \\ (x+1)(x-2) & = 0 \\ x=-1 & \vee x =2 \end{align*}$
$\spadesuit \, $ Luas daerah arsiran
$\begin{align*} \text{L}_\text{arsir} & = L_A + L_B \\ & = \int \limits_{-2}^{-1} (x+2) dx + \int \limits_{-1}^0 x^2 dx \end{align*}$
Jadi, Luasnya adalah $\int \limits_{-2}^{-1} (x+2) dx + \int \limits_{-1}^0 x^2 dx . \heartsuit $

$\spadesuit \, $ Titik potong kedua kurva
$\begin{align*} y_1 & = y_2 \\ x^2 & = x + 2 \\ x^2 - x- 2 & = 0 \\ (x+1)(x-2) & = 0 \\ x=-1 & \vee x =2 \end{align*}$
$\spadesuit \, $ Luas daerah arsiran
$\begin{align*} \text{L}_\text{arsir} & = L_A + L_B \\ & = \int \limits_{-2}^{-1} (x+2) dx + \int \limits_{-1}^0 x^2 dx \end{align*}$
Jadi, Luasnya adalah $\int \limits_{-2}^{-1} (x+2) dx + \int \limits_{-1}^0 x^2 dx . \heartsuit $
terimakasih atas penjelasnnya sangat membantu tapi saya masih bingung dengan penjelasan nomor 10. R di daerah kuadran satu kenapa Luas daerahnya ada di x negatif (kuadran 2) mhon penjelasannya. terimkasih
BalasHapushallow naily.
Hapuswah, terima kasih untuk pertanyaannya.
ternyata benar, untuk soal nomor 10, ternyata yang ditanya daerah dikuadran satu.
setelah saya cek lagi ke soal aslinya, memang yang ditanyakan di kuadran satu, dan saya hitung lagi dan cek daerahnya tenyata tidak ada jawabannya di pilihannya.
mungkin di soal salah ketik, soal ini saya dapat dari download di internet, mungkin saja orang pertama yang menyebarkannya salah ketik.
jika ditanyakan didaerah kuadran dua, maka jawabannya sudah benar seperti tertulis di atas.
terima kasih untuk pertanyaan sekaligus koreksinya....
Mudah-mudahan saya bisa menemukan soal aslinya, dan akan saya share lagi kalau ada perubahannya.