Nomor 11
Diketahui segitiga ABC dengan AB = 1 cm, BC = 2 cm, dan AC = $k $ cm. Jika $\alpha $ adalah sudut ACB, maka nilai $k $ yang memenuhi
$\cos \alpha < \frac{7}{8} $ adalah ....
$\clubsuit \, $ Gambar

Interval nilai $k$ agar terbentuk segitiga ABC :
$2-1 < k < 2+1 \leftrightarrow HP_1 = \{ 1 < k < 3 \} $
$\clubsuit \, $ Aturan cosinus
$\begin{align*} AB^2 & = CB^2 + CA^2 - 2.CB.CA.\cos \alpha \\ \cos \alpha & = \frac{CB^2 + CA^2 - AB^2}{2.CB.CA} \\ \cos \alpha & = \frac{2^2 + k^2 - 1^2}{2.2.k} = \frac{k^2 + 3}{4k} \end{align*}$
$\clubsuit \, $ Menyelesaikan pertidaksamaan
$\begin{align*} \cos \alpha & < \frac{7}{8} \\ \frac{k^2 + 3}{4k} & < \frac{7}{8} \\ \frac{k^2 + 3}{4k} - \frac{7}{8} & < 0 \\ \frac{2k^2 - 7k + 6}{8k} & < 0 \\ \frac{(2k-3)(k-2)}{8k} & < 0 \\ k=\frac{3}{2}, \, & k =2 , \, k =0 \end{align*}$

$HP_2 = \{ k < 0 \vee \frac{3}{2} < k < 2 \} $
Sehingga solusinya :
$ HP = HP_1 \cap HP_2 = \{ \frac{3}{2} < k < 2 \} $
Jadi, nilai $k$ adalah $ \{ \frac{3}{2} < k < 2 \}. \heartsuit $

Interval nilai $k$ agar terbentuk segitiga ABC :
$2-1 < k < 2+1 \leftrightarrow HP_1 = \{ 1 < k < 3 \} $
$\clubsuit \, $ Aturan cosinus
$\begin{align*} AB^2 & = CB^2 + CA^2 - 2.CB.CA.\cos \alpha \\ \cos \alpha & = \frac{CB^2 + CA^2 - AB^2}{2.CB.CA} \\ \cos \alpha & = \frac{2^2 + k^2 - 1^2}{2.2.k} = \frac{k^2 + 3}{4k} \end{align*}$
$\clubsuit \, $ Menyelesaikan pertidaksamaan
$\begin{align*} \cos \alpha & < \frac{7}{8} \\ \frac{k^2 + 3}{4k} & < \frac{7}{8} \\ \frac{k^2 + 3}{4k} - \frac{7}{8} & < 0 \\ \frac{2k^2 - 7k + 6}{8k} & < 0 \\ \frac{(2k-3)(k-2)}{8k} & < 0 \\ k=\frac{3}{2}, \, & k =2 , \, k =0 \end{align*}$

$HP_2 = \{ k < 0 \vee \frac{3}{2} < k < 2 \} $
Sehingga solusinya :
$ HP = HP_1 \cap HP_2 = \{ \frac{3}{2} < k < 2 \} $
Jadi, nilai $k$ adalah $ \{ \frac{3}{2} < k < 2 \}. \heartsuit $
Nomor 12
Nilai $m+n $ yang mengakibatkan $x^4-6ax^3+8a^2x^2-ma^3x+na^4 $ habis dibagi $(x-a)^2 $ adalah ....
$\spadesuit \, $ Habis dibagi, artinya sisanya 0.
$x^4-6ax^3+8a^2x^2-ma^3x+na^4 \, : \, (x-a)^2 $
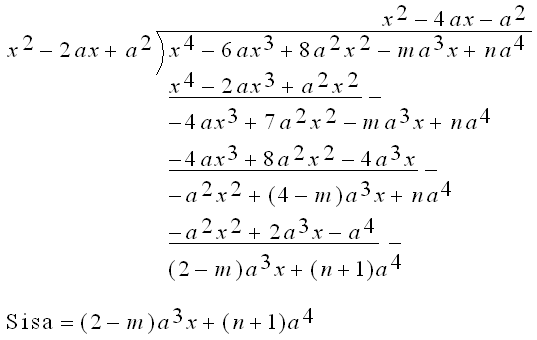
$\spadesuit \, $ Agar sisanya 0, haruslah :
$(2-m)a^3 = 0 \rightarrow m=2 \vee a = 0 $
$(n+1)a^4 = 0 \rightarrow n=-1 \vee a = 0 $
Sehingga $m+n = 2 + (-1) = 1 $
Jadi, nilai $m+n = 1 . \heartsuit $
$x^4-6ax^3+8a^2x^2-ma^3x+na^4 \, : \, (x-a)^2 $
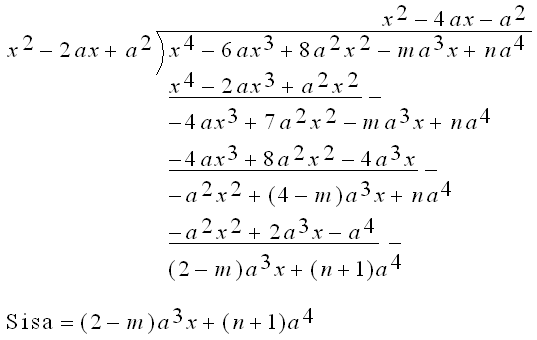
$\spadesuit \, $ Agar sisanya 0, haruslah :
$(2-m)a^3 = 0 \rightarrow m=2 \vee a = 0 $
$(n+1)a^4 = 0 \rightarrow n=-1 \vee a = 0 $
Sehingga $m+n = 2 + (-1) = 1 $
Jadi, nilai $m+n = 1 . \heartsuit $
Nomor 13
Jumlah nilai-nilai $m $ yang mengakibatkan persamaan kuadrat $mx^2-(3m+1)x+(2m+2) = 0 $ mempunyai akar-akar perbadingan dengan
perbandingan 3 : 4 adalah ....
$\spadesuit \, $ Misalkan akar-akarnya $x_1 $ dan $x_2 $
$\frac{x_1}{x_2} = \frac{3}{4} \rightarrow x_1 = \frac{3}{4} x_2 $ ....pers(i)
$\spadesuit \, $ Operasi penjumlahan dan pers(i)
$\begin{align*} x_1 + x_2 & = \frac{-b}{a} \\ \frac{3}{4} x_2 + x_2 & = \frac{3m+1}{m} \\ \frac{7}{4} x_2 & = \frac{3m+1}{m} \\ x_2 & = \frac{3m+1}{m} . \frac{4}{7} = \frac{4(3m+1)}{7m} \end{align*}$
$\spadesuit \, $ Substitusi $x_2= \frac{4(3m+1)}{7m} $ ke persamaan kuadrat
$\begin{align*} mx^2-(3m+1)x+(2m+2) & = 0 \\ m\left( \frac{4(3m+1)}{7m} \right)^2-(3m+1).\left( \frac{4(3m+1)}{7m} \right)+(2m+2) & = 0 \\ 5m^2-13m+6 & = 0 \end{align*}$
jumlah nilai $m$ :
$m_1+m_2 = \frac{-b}{a} = \frac{13}{5} $
Jadi, jumlah nilai $m$ adalah $\frac{13}{5}. \heartsuit $
$\frac{x_1}{x_2} = \frac{3}{4} \rightarrow x_1 = \frac{3}{4} x_2 $ ....pers(i)
$\spadesuit \, $ Operasi penjumlahan dan pers(i)
$\begin{align*} x_1 + x_2 & = \frac{-b}{a} \\ \frac{3}{4} x_2 + x_2 & = \frac{3m+1}{m} \\ \frac{7}{4} x_2 & = \frac{3m+1}{m} \\ x_2 & = \frac{3m+1}{m} . \frac{4}{7} = \frac{4(3m+1)}{7m} \end{align*}$
$\spadesuit \, $ Substitusi $x_2= \frac{4(3m+1)}{7m} $ ke persamaan kuadrat
$\begin{align*} mx^2-(3m+1)x+(2m+2) & = 0 \\ m\left( \frac{4(3m+1)}{7m} \right)^2-(3m+1).\left( \frac{4(3m+1)}{7m} \right)+(2m+2) & = 0 \\ 5m^2-13m+6 & = 0 \end{align*}$
jumlah nilai $m$ :
$m_1+m_2 = \frac{-b}{a} = \frac{13}{5} $
Jadi, jumlah nilai $m$ adalah $\frac{13}{5}. \heartsuit $
Nomor 14
Jika $a^2 $ dan $b $ adalah akar-akar persamaan kuadrat $x^2-(b^2-1)x+b=0 $ . Himpunan nilai-nilai $a+b $ adalah ....
$\spadesuit \, $ PK : $x^2-(b^2-1)x+b=0 \, \, \, $ akar-akarnya $x_1 = a^2 $ dan $x_2 = b $
$\spadesuit \, $ Operasi perkalian
$\begin{align*} x_1 . x_2 & = \frac{c}{a} \\ a^2 . b & = \frac{b}{1} \\ a^2 & = 1 \rightarrow a = \pm 1 \end{align*}$
$\spadesuit \, $ Operasi pehjumlahan
$\begin{align*} x_1 + x_2 & = \frac{-b}{a} \\ a^2 + b & = \frac{b^2-1}{1} \, \, \, \text{(nilai } \, a^2 = 1 \, ) \\ 1 + b & = b^2 - 1 \\ b^2-b-2 & = 0 \\ (b+1)(b-2) & = 0 \\ b=-1 & \vee b = 2 \end{align*}$
$\spadesuit \, $ Menentukan nilai $a+b$
$a=1, b=-1 \rightarrow a+b = 1 + (-1) = 0 $
$a=1, b=2 \rightarrow a+b = 1 + 2 = 3 $
$a=-1, b=-1 \rightarrow a+b = -1 + (-1) = -2 $
$a=-1, b=2 \rightarrow a+b = -1 + 2 = 1 $
Jadi, himpunan nilai $a+b\, \, $ adalah $\{ -2, 0, 1, 3 \} . \heartsuit $
$\spadesuit \, $ Operasi perkalian
$\begin{align*} x_1 . x_2 & = \frac{c}{a} \\ a^2 . b & = \frac{b}{1} \\ a^2 & = 1 \rightarrow a = \pm 1 \end{align*}$
$\spadesuit \, $ Operasi pehjumlahan
$\begin{align*} x_1 + x_2 & = \frac{-b}{a} \\ a^2 + b & = \frac{b^2-1}{1} \, \, \, \text{(nilai } \, a^2 = 1 \, ) \\ 1 + b & = b^2 - 1 \\ b^2-b-2 & = 0 \\ (b+1)(b-2) & = 0 \\ b=-1 & \vee b = 2 \end{align*}$
$\spadesuit \, $ Menentukan nilai $a+b$
$a=1, b=-1 \rightarrow a+b = 1 + (-1) = 0 $
$a=1, b=2 \rightarrow a+b = 1 + 2 = 3 $
$a=-1, b=-1 \rightarrow a+b = -1 + (-1) = -2 $
$a=-1, b=2 \rightarrow a+b = -1 + 2 = 1 $
Jadi, himpunan nilai $a+b\, \, $ adalah $\{ -2, 0, 1, 3 \} . \heartsuit $
Nomor 15
Perhatikan kurva $y=ax+bx^2, \, \, a $ dan $b $ konstan. Jika garis singgung kurva ini pada titik (1, 0) sejajar dengan garis
$2x-y+3=0 $ , maka $a+3b $ sama dengan ....
$\clubsuit \, $ gradien garis : $2x-y+3=0 \rightarrow m_1 = \frac{-a}{b} = \frac{-2}{-1} = 2$
Karena sejajar, maka gradiennya sama : $ m = m_1 = 2 $
$\clubsuit \, $ Gradien garis singgung di titik (1,0)
$\begin{align*} y & = ax+bx^2 \\ y^\prime & = a + 2bx \\ m & = f^\prime (1) \\ 2 & = a + 2b.(1) \\ a+2b & = 2 \, \, \, \text{...pers(i)} \end{align*}$
$\clubsuit \, $ Substitusi (1,0) ke kurva
$y=ax+bx^2 \rightarrow 0 = a.1 + b.1^2 \rightarrow a+b = 0 \, \, \, \text{...pers(ii)} $
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} a+2b = 2 & \\ a+b = 0 & - \\ \hline b=2, a = -2 & \end{array} $
Jadi, nilai $a+3b = -2+3.2 = 4 . \heartsuit $
Karena sejajar, maka gradiennya sama : $ m = m_1 = 2 $
$\clubsuit \, $ Gradien garis singgung di titik (1,0)
$\begin{align*} y & = ax+bx^2 \\ y^\prime & = a + 2bx \\ m & = f^\prime (1) \\ 2 & = a + 2b.(1) \\ a+2b & = 2 \, \, \, \text{...pers(i)} \end{align*}$
$\clubsuit \, $ Substitusi (1,0) ke kurva
$y=ax+bx^2 \rightarrow 0 = a.1 + b.1^2 \rightarrow a+b = 0 \, \, \, \text{...pers(ii)} $
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} a+2b = 2 & \\ a+b = 0 & - \\ \hline b=2, a = -2 & \end{array} $
Jadi, nilai $a+3b = -2+3.2 = 4 . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.