Nomor 6
Agung mempunyai satu bundel tiket piala dunia untuk dijual. Pada hari pertama terjual sepuluh lembar tiket, hari kedua terjual setengah
dari tiket yang tersisa, dan pada hari ketiga terjual 5 lembar tiket. Jika tersisa 2 lembar tiket, maka banyaknya tiket dalam satu
bundel adalah ....
$\spadesuit \, $ Jumlah awal tiket dalam satu bundel sebanyak $x$
Hari I : terjual 10 tiket
Sisa I = $x-10$
Hari II : terjual setengah
Sisa II = $\frac{1}{2}(x-10) $
Hari III : terjual 5 tiket
Sisa III = $\frac{1}{2}(x-10) - 5 = \frac{1}{2}x - 10 $
$\spadesuit \, $ Sisa tiket di hari III adalah 2
$\begin{align} \text{Sisa III} \, & = 2 \\ \frac{1}{2}x - 10 & = 2 \\ \frac{1}{2}x & = 12 \\ x & = 24 \end{align}$
Jadi, banyak tiket dalam satu bundel sebanyak 24 buah. $ \heartsuit $
Hari I : terjual 10 tiket
Sisa I = $x-10$
Hari II : terjual setengah
Sisa II = $\frac{1}{2}(x-10) $
Hari III : terjual 5 tiket
Sisa III = $\frac{1}{2}(x-10) - 5 = \frac{1}{2}x - 10 $
$\spadesuit \, $ Sisa tiket di hari III adalah 2
$\begin{align} \text{Sisa III} \, & = 2 \\ \frac{1}{2}x - 10 & = 2 \\ \frac{1}{2}x & = 12 \\ x & = 24 \end{align}$
Jadi, banyak tiket dalam satu bundel sebanyak 24 buah. $ \heartsuit $
Nomor 7
Jika ($a,b,c$) adalah solusi sistem persamaan linear :
$\left\{ \begin{array}{c} x+y+2z=9 \\ 2x+4y-3z=1 \\ 3x+6y-5z=0 \end{array} \right. $
Maka $a+b+c = ....$
$\left\{ \begin{array}{c} x+y+2z=9 \\ 2x+4y-3z=1 \\ 3x+6y-5z=0 \end{array} \right. $
Maka $a+b+c = ....$
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{c|c|cc} x+y+2z=9 & \text{kali 2} & 2x+2y+4z=18 & \\ 2x+4y-3z=1 & \text{kali 1} & 2x+4y-3z=1 & - \\ \hline & & -2y+7z=17 & (iv) \end{array}$
$\clubsuit \, $ Eliminasi pers(i) dan pers(iii)
$\begin{array}{c|c|cc} x+y+2z=9 & \text{kali 3} & 3x+3y+6z=27 & \\ 3x+6y-5z=0 & \text{kali 1} & 3x+6y-5z=0 & - \\ \hline & & -3y+11z=27 & (v) \end{array}$
$\clubsuit \, $ Eliminasi pers(iv) dan pers(v)
$\begin{array}{c|c|cc} -2y+7z=17 & \text{kali 3} & -6y+21z=51 & \\ -3y+11z=27 & \text{kali 2} & -6y+22z=54 & - \\ \hline & & z=3 & \end{array}$
$\clubsuit \, $ pers(iv)
$ -2y+7z=17 \rightarrow -2y+7.(3)=17 \rightarrow y = 1 $
$\clubsuit \, $ pers(i)
$ x+y+2z=9 \rightarrow x+1+2.(3)=9 \rightarrow x = 2 $
sehingga : $a=x=2,b=y=1,c=z=3 \rightarrow a+b+c= 2+1+3 = 6 $
Jadi, nilai $ a+b+c = 6. \heartsuit$
$\begin{array}{c|c|cc} x+y+2z=9 & \text{kali 2} & 2x+2y+4z=18 & \\ 2x+4y-3z=1 & \text{kali 1} & 2x+4y-3z=1 & - \\ \hline & & -2y+7z=17 & (iv) \end{array}$
$\clubsuit \, $ Eliminasi pers(i) dan pers(iii)
$\begin{array}{c|c|cc} x+y+2z=9 & \text{kali 3} & 3x+3y+6z=27 & \\ 3x+6y-5z=0 & \text{kali 1} & 3x+6y-5z=0 & - \\ \hline & & -3y+11z=27 & (v) \end{array}$
$\clubsuit \, $ Eliminasi pers(iv) dan pers(v)
$\begin{array}{c|c|cc} -2y+7z=17 & \text{kali 3} & -6y+21z=51 & \\ -3y+11z=27 & \text{kali 2} & -6y+22z=54 & - \\ \hline & & z=3 & \end{array}$
$\clubsuit \, $ pers(iv)
$ -2y+7z=17 \rightarrow -2y+7.(3)=17 \rightarrow y = 1 $
$\clubsuit \, $ pers(i)
$ x+y+2z=9 \rightarrow x+1+2.(3)=9 \rightarrow x = 2 $
sehingga : $a=x=2,b=y=1,c=z=3 \rightarrow a+b+c= 2+1+3 = 6 $
Jadi, nilai $ a+b+c = 6. \heartsuit$
Nomor 8
Solusi pertaksamaan $\frac{(x-2)(x^2+x-6)}{x^2+x-20} > 0 $ adalah ....
$\spadesuit \, $ Menentukan akar-akarnya
$\begin{align*} \frac{(x-2)(x^2+x-6)}{x^2+x-20} & > 0 \\ \frac{(x-2)(x-2)(x+3)}{(x-4)(x+5)} & > 0 \\ x=2, x=-3, x & = 4, x=-5 \end{align*}$
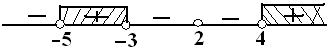
Jadi, $HP = \{-5< x < -3 \vee x > 4 \} \heartsuit$
$\begin{align*} \frac{(x-2)(x^2+x-6)}{x^2+x-20} & > 0 \\ \frac{(x-2)(x-2)(x+3)}{(x-4)(x+5)} & > 0 \\ x=2, x=-3, x & = 4, x=-5 \end{align*}$
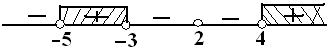
Jadi, $HP = \{-5< x < -3 \vee x > 4 \} \heartsuit$
Nomor 9
Solusi pertaksamaan $\frac{2x^2+x-3}{6x^2+x-1} < 0 $ adalah ....
$\clubsuit \, $ Menentukan akar-akarnya
$\begin{align*} \frac{2x^2+x-3}{6x^2+x-1} & < 0 \\ \frac{(2x+3)(x-1)}{(2x+1)(3x-1)} & < 0 \\ x=-\frac{3}{2}, x=1, x & = -\frac{1}{2}, x=\frac{1}{3} \end{align*}$
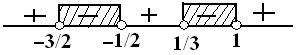
Jadi, $HP = \{-\frac{3}{2} < x < -\frac{1}{2} \vee \frac{1}{3} < x < 1 \} \heartsuit$
$\begin{align*} \frac{2x^2+x-3}{6x^2+x-1} & < 0 \\ \frac{(2x+3)(x-1)}{(2x+1)(3x-1)} & < 0 \\ x=-\frac{3}{2}, x=1, x & = -\frac{1}{2}, x=\frac{1}{3} \end{align*}$
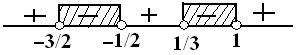
Jadi, $HP = \{-\frac{3}{2} < x < -\frac{1}{2} \vee \frac{1}{3} < x < 1 \} \heartsuit$
Nomor 10
Suku ke-$n$ suatu barisan geometri adalah $U_n $ . Jika $U_1 = k, \, U_2=3k, \, \, $ dan $U_3=8k+4 , \, $ maka $ U_5=....$
$\spadesuit \, $ Barisan geometri : Rasio sama
$\begin{align} \frac{U_2}{U_1} & = \frac{U_3}{U_2} \\ \frac{3k}{k} & = \frac{8k+4}{3k} \\ 3 & = \frac{8k+4}{3k} \\ 9k & = 8k + 4 \\ k & = 4 \end{align}$
$\spadesuit \, $ Substitusi nilai $k=4 $ ke barisannnya, menjadi :
Barisannya : 4, 12, 36 $\rightarrow r = \frac{12}{4} = 3 $
$\spadesuit \, $ Menentukan suku kelima
$U_5 = ar^4 = 4. (3)^4 = 4.81 = 324 $
Jadi, nilai $U_5 = 324. \heartsuit $
$\begin{align} \frac{U_2}{U_1} & = \frac{U_3}{U_2} \\ \frac{3k}{k} & = \frac{8k+4}{3k} \\ 3 & = \frac{8k+4}{3k} \\ 9k & = 8k + 4 \\ k & = 4 \end{align}$
$\spadesuit \, $ Substitusi nilai $k=4 $ ke barisannnya, menjadi :
Barisannya : 4, 12, 36 $\rightarrow r = \frac{12}{4} = 3 $
$\spadesuit \, $ Menentukan suku kelima
$U_5 = ar^4 = 4. (3)^4 = 4.81 = 324 $
Jadi, nilai $U_5 = 324. \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.