Nomor 11
Panjang sisi sebuah segitiga siku-siku membentuk barisan aritmetika. Jika keliling segitiga tersebut adalah 72, maka luasnya
adalah ....
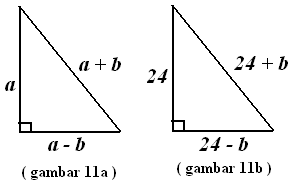
$\spadesuit \, $ Misalkan sisinya : $a-b, a, a+b \, \, \, $ (seperti gambar 11a di bawah)
$\begin{align} \text{Keliling} \, \Delta & = 72 \\ (a-b) + a + (a+b) & = 72 \\ 3a & = 72 \rightarrow a = 24 \end{align}$
Substitusi $a=24 $ ke segitiga seperti gambar 11b
$\spadesuit \, $ Teorema Pythagoras pada segitiga
$\begin{align} (24+b)^2 & = 24^2 + (24-b)^2 \\ (24+b)^2 - (24-b)^2 & = 24\times 24 \\ [(24+b)-(24-b)][(24+b)+(24-b)] & = 24\times 24 \\ 2b \times 48 & = 24\times 24 \rightarrow b = 8 \end{align}$
Sehingga : tinggi = 24 dan alas = 24 - b = 24 - 6 = 18
Luas $\Delta = \frac{1}{2} . a . t = \frac{1}{2}.18.24 = 216 $
Jadi, luas segitiganya adalah 216. $ \heartsuit $

$\begin{align} \text{Keliling} \, \Delta & = 72 \\ (a-b) + a + (a+b) & = 72 \\ 3a & = 72 \rightarrow a = 24 \end{align}$
Substitusi $a=24 $ ke segitiga seperti gambar 11b
$\spadesuit \, $ Teorema Pythagoras pada segitiga
$\begin{align} (24+b)^2 & = 24^2 + (24-b)^2 \\ (24+b)^2 - (24-b)^2 & = 24\times 24 \\ [(24+b)-(24-b)][(24+b)+(24-b)] & = 24\times 24 \\ 2b \times 48 & = 24\times 24 \rightarrow b = 8 \end{align}$
Sehingga : tinggi = 24 dan alas = 24 - b = 24 - 6 = 18
Luas $\Delta = \frac{1}{2} . a . t = \frac{1}{2}.18.24 = 216 $
Jadi, luas segitiganya adalah 216. $ \heartsuit $
Cara II
$\spadesuit \, $ Triple pythagoras yang membentuk barisan aritmetika : 3, 4, 5

$\begin{align} \text{Keliling} \, \Delta & = 72 \\ 3x+4x+5x & = 72 \\ 12x & = 72 \rightarrow x = 6 \end{align}$
Sehingga : tinggi = $4x=4.6=24 \, \, $ dan alas = $3x=3.6 = 18 $
Luas $\Delta = \frac{1}{2} . a . t = \frac{1}{2}.18.24 = 216 $
Jadi, luas segitiganya adalah 216. $ \heartsuit $
$\spadesuit \, $ Triple pythagoras yang membentuk barisan aritmetika : 3, 4, 5

$\begin{align} \text{Keliling} \, \Delta & = 72 \\ 3x+4x+5x & = 72 \\ 12x & = 72 \rightarrow x = 6 \end{align}$
Sehingga : tinggi = $4x=4.6=24 \, \, $ dan alas = $3x=3.6 = 18 $
Luas $\Delta = \frac{1}{2} . a . t = \frac{1}{2}.18.24 = 216 $
Jadi, luas segitiganya adalah 216. $ \heartsuit $
Nomor 12
Untuk membuat barang A diperlukan 6 jam kerja mesin I dan 4 jam kerja mesin II. Sedangkan untuk barang B diperlukan 4 jam kerja mesin I
dan 8 jam kerja mesin II. Setiap hari kedua mesin tersebut bekerja tidak lebih dari 18 jam. Jika setiap hari dapat dihasilkan
$x$ barang A dan $y$ barang B, maka model matematikanya adalah ....
$\clubsuit \, $ Tabelnya

$\clubsuit \, $ Model matematikanya
$6x+4y \leq 18 \rightarrow 3x+2y \leq 9 $
$4x+8y \leq 18 \rightarrow 2x+4y \leq 9 $
$x \geq 0 , y \geq 0 $
Jadi, modelnya : $ 3x+2y \leq 9 , 2x+4y \leq 9 , x \geq 0 , y \geq 0 . \heartsuit $

$\clubsuit \, $ Model matematikanya
$6x+4y \leq 18 \rightarrow 3x+2y \leq 9 $
$4x+8y \leq 18 \rightarrow 2x+4y \leq 9 $
$x \geq 0 , y \geq 0 $
Jadi, modelnya : $ 3x+2y \leq 9 , 2x+4y \leq 9 , x \geq 0 , y \geq 0 . \heartsuit $
Nomor 13
Jika invers dari $A = \left( \begin{matrix} a & 1+a \\ 0 & a \end{matrix} \right) $ adalah $A^{-1} = \left( \begin{matrix} 1 & b \\ 0 & 1 \end{matrix} \right) $ ,
maka konstanta $b$ adalah ....
$\spadesuit \, $ Sifat invers matriks : $(A^{-1})^{-1} = A $
Invers matriks $A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow A^{-1} = \frac{1}{ad-bc} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right)$
$\begin{align} (A^{-1})^{-1} & = A \\ \left( \begin{matrix} 1 & b \\ 0 & 1 \end{matrix} \right)^{-1} & = \left( \begin{matrix} a & 1+a \\ 0 & a \end{matrix} \right) \\ \frac{1}{1.1-0.b} \left( \begin{matrix} 1 & -b \\ 0 & 1 \end{matrix} \right) & = \left( \begin{matrix} a & 1+a \\ 0 & a \end{matrix} \right) \\ \frac{1}{1}\left( \begin{matrix} 1 & -b \\ 0 & 1 \end{matrix} \right) & = \left( \begin{matrix} a & 1+a \\ 0 & a \end{matrix} \right) \\ a & =1 \\ -b & = 1 + a \\ -b & = 1 + 1 \rightarrow b =-2 \end{align}$
Jadi, nilai $ b = -2 . \heartsuit $
Invers matriks $A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow A^{-1} = \frac{1}{ad-bc} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right)$
$\begin{align} (A^{-1})^{-1} & = A \\ \left( \begin{matrix} 1 & b \\ 0 & 1 \end{matrix} \right)^{-1} & = \left( \begin{matrix} a & 1+a \\ 0 & a \end{matrix} \right) \\ \frac{1}{1.1-0.b} \left( \begin{matrix} 1 & -b \\ 0 & 1 \end{matrix} \right) & = \left( \begin{matrix} a & 1+a \\ 0 & a \end{matrix} \right) \\ \frac{1}{1}\left( \begin{matrix} 1 & -b \\ 0 & 1 \end{matrix} \right) & = \left( \begin{matrix} a & 1+a \\ 0 & a \end{matrix} \right) \\ a & =1 \\ -b & = 1 + a \\ -b & = 1 + 1 \rightarrow b =-2 \end{align}$
Jadi, nilai $ b = -2 . \heartsuit $
Nomor 14
Jika data $2,a,a,3,4,6 $ mempunyai rataan $c $ . Dan data $2,c,c,4,6,2,1 $ mempunyai rataan $2a$ , maka nilai $c$ adalah ....
$\clubsuit \,$ Rataan pertama
$\begin{align} \frac{2+a+a+3+4+6}{6} & = c \\ 2a + 15 & = 6c \\ 2a - 6c & = -15 \, \, \, \text{...pers(i)} \end{align}$
$\clubsuit \,$ Rataan kedua
$\begin{align} \frac{2+c+c+4+6+2+1}{7} & = 2a \\ 2c + 15 & = 14a \\ 14a - 2c & = 15 \, \, \, \text{...pers(ii)} \end{align}$
$\clubsuit \,$ Eliminasi pers(i) dan pers(ii)
$\begin{array}{c|c|cc} 2a - 6c = -15 & \times 7 & 14a - 42c = -105 & \\ 14a - 2c = 15 & \times 1 & 14a - 2c = 15 & - \\ \hline & & -40c = -120 \rightarrow c=3 & \end{array} $
Jadi, nilai $ c=3. \heartsuit $
$\begin{align} \frac{2+a+a+3+4+6}{6} & = c \\ 2a + 15 & = 6c \\ 2a - 6c & = -15 \, \, \, \text{...pers(i)} \end{align}$
$\clubsuit \,$ Rataan kedua
$\begin{align} \frac{2+c+c+4+6+2+1}{7} & = 2a \\ 2c + 15 & = 14a \\ 14a - 2c & = 15 \, \, \, \text{...pers(ii)} \end{align}$
$\clubsuit \,$ Eliminasi pers(i) dan pers(ii)
$\begin{array}{c|c|cc} 2a - 6c = -15 & \times 7 & 14a - 42c = -105 & \\ 14a - 2c = 15 & \times 1 & 14a - 2c = 15 & - \\ \hline & & -40c = -120 \rightarrow c=3 & \end{array} $
Jadi, nilai $ c=3. \heartsuit $
Nomor 15
Dalam $\Delta$ABC , jika D pada AB sehingga CD$\bot \, $AB, BC = $a$ , $\angle$CAB = 60$^\circ$ , $\angle$ABC = 45$^\circ$ maka AD = ....
$\spadesuit \, $ Gambar

$\spadesuit \, $ Segitiga BCD
$\begin{align} \sin CBD & = \frac{CD}{BC} \\ CD & = BC . \sin CBD \\ CD & = a . \sin 45^\circ = a. \frac{1}{2}\sqrt{2} = \frac{1}{2} a \sqrt{2} \end{align}$
$\spadesuit \, $ Segitiga ACD
$\begin{align} \tan CAD & = \frac{CD}{AD} \\ AD & = \frac{CD}{\tan CAD} \\ AD & = \frac{\frac{1}{2} a \sqrt{2}}{\tan 60^\circ } = \frac{\frac{1}{2} a \sqrt{2}}{\sqrt{3}} = \frac{1}{6} a \sqrt{6} \\ \end{align}$
Jadi, panjang $ AD = \frac{1}{6} a \sqrt{6} .\heartsuit $

$\spadesuit \, $ Segitiga BCD
$\begin{align} \sin CBD & = \frac{CD}{BC} \\ CD & = BC . \sin CBD \\ CD & = a . \sin 45^\circ = a. \frac{1}{2}\sqrt{2} = \frac{1}{2} a \sqrt{2} \end{align}$
$\spadesuit \, $ Segitiga ACD
$\begin{align} \tan CAD & = \frac{CD}{AD} \\ AD & = \frac{CD}{\tan CAD} \\ AD & = \frac{\frac{1}{2} a \sqrt{2}}{\tan 60^\circ } = \frac{\frac{1}{2} a \sqrt{2}}{\sqrt{3}} = \frac{1}{6} a \sqrt{6} \\ \end{align}$
Jadi, panjang $ AD = \frac{1}{6} a \sqrt{6} .\heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.