Nomor 6
Nilai maksimum dari $f(x,y) = 10x+20y \, $ dengan kendala $x \geq 0, y \geq 0, x+4y \leq 120, x+y \leq 60 \, $ adalah ....
$\spadesuit \, $ Gambar daerah penyelesaian dan titik potong kedua garis
$ x+4y \leq 120 \rightarrow (0,30), \, (120,0) $
$ x+y \leq 60 \rightarrow (0,60), \, (60,0) $
titik potong kedua garis dengan eliminasi
$\begin{array}{cc} x+4y = 120 & \\ x+y = 60 & - \\ \hline 3y = 60 \rightarrow y=20 \end{array} $
$x+y=60 \rightarrow x+20 = 60 \rightarrow x = 40 $
sehingga titik potong kedua garis : (40, 20)
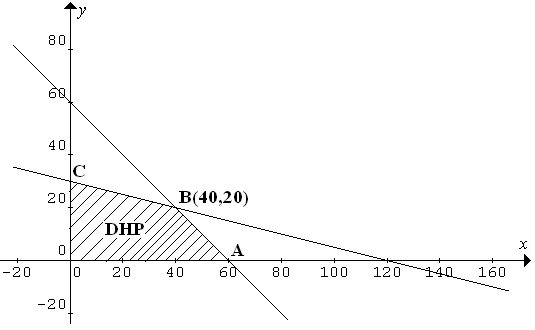
$\spadesuit \, $ Substitusi semua titik pojok ke fungsi tujuan : $f(x,y) = 10x+20y $
A(60,0) $\rightarrow \, f = 10.60 + 20.0 = 600 $
B(40,20) $\rightarrow \, f = 10.40 + 20.20 = 800 $
C(0,30) $\rightarrow \, f = 10.0 + 20.30 = 600 $
Jadi, nilai maksimumnya adalah 800. $ \heartsuit $
$ x+4y \leq 120 \rightarrow (0,30), \, (120,0) $
$ x+y \leq 60 \rightarrow (0,60), \, (60,0) $
titik potong kedua garis dengan eliminasi
$\begin{array}{cc} x+4y = 120 & \\ x+y = 60 & - \\ \hline 3y = 60 \rightarrow y=20 \end{array} $
$x+y=60 \rightarrow x+20 = 60 \rightarrow x = 40 $
sehingga titik potong kedua garis : (40, 20)

$\spadesuit \, $ Substitusi semua titik pojok ke fungsi tujuan : $f(x,y) = 10x+20y $
A(60,0) $\rightarrow \, f = 10.60 + 20.0 = 600 $
B(40,20) $\rightarrow \, f = 10.40 + 20.20 = 800 $
C(0,30) $\rightarrow \, f = 10.0 + 20.30 = 600 $
Jadi, nilai maksimumnya adalah 800. $ \heartsuit $
Nomor 7
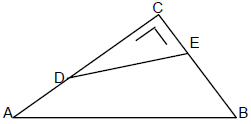
Jika $\Delta$ABC siku-siku samakaki, AC = BC = 4, dan AD = CE, maka luas minimum dari segiempat ABED adalah ....

Jika $\Delta$ABC siku-siku samakaki, AC = BC = 4, dan AD = CE, maka luas minimum dari segiempat ABED adalah ....
$\clubsuit \, $ Misalkan : CE = $x $ , maka AD = $x $ , dan CD = $4-x$
$\begin{align} L_{ABED} \, & = L_{ABC} - L_{CDE} \\ L & = \frac{1}{2}.4.4 - \frac{1}{2}.x.(4-x) \\ L & = 8-2x+\frac{1}{2}x^2 \\ L^\prime & = -2+x \end{align} $
$\clubsuit \, $ Luas minimum : $L^\prime = 0 \, \, $ (turunan = 0 )
$L^\prime = 0 \rightarrow -2+x = 0 \rightarrow x = 2 $
sehingga : $ L = 8-2x+\frac{1}{2}x^2 = 8-2.2+\frac{1}{2}.2^2 = 8-4+2 = 6 $
Jadi, luas minimumnya adalah 6 . $ \heartsuit$
$\begin{align} L_{ABED} \, & = L_{ABC} - L_{CDE} \\ L & = \frac{1}{2}.4.4 - \frac{1}{2}.x.(4-x) \\ L & = 8-2x+\frac{1}{2}x^2 \\ L^\prime & = -2+x \end{align} $
$\clubsuit \, $ Luas minimum : $L^\prime = 0 \, \, $ (turunan = 0 )
$L^\prime = 0 \rightarrow -2+x = 0 \rightarrow x = 2 $
sehingga : $ L = 8-2x+\frac{1}{2}x^2 = 8-2.2+\frac{1}{2}.2^2 = 8-4+2 = 6 $
Jadi, luas minimumnya adalah 6 . $ \heartsuit$
Cara II
$\clubsuit \, $ Untuk keadaan seperti gambar
Luas minimumnya : $L_{ABED} = \frac{3}{4}. L_{ABC} $
$L = \frac{3}{4}. L_{ABC} = \frac{3}{4}. \frac{1}{2} . 4. 4 = 6 $
Jadi, luas minimumnya adalah 6 . $ \heartsuit$
$\clubsuit \, $ Untuk keadaan seperti gambar
Luas minimumnya : $L_{ABED} = \frac{3}{4}. L_{ABC} $
$L = \frac{3}{4}. L_{ABC} = \frac{3}{4}. \frac{1}{2} . 4. 4 = 6 $
Jadi, luas minimumnya adalah 6 . $ \heartsuit$
Nomor 8
Jika $2\tan ^2 x + 3 \tan x - 2 = 0, \, \frac{1}{2}\pi < x < \pi, \, $ maka $\sin x + \cos x = .... $
$\spadesuit \, $ Menentukan nilai $\tan x $
$\begin{align*} 2\tan ^2 x + 3 \tan x - 2 & = 0 \\ (2\tan x -1)(\tan x + 2) & = 0 \\ \tan x = \frac{1}{2} & \vee \tan x = -2 \end{align*}$
Karena $x \, $ dikuadran II , maka nilai $\tan x \, \, $ harus negatif, sehingga yang memenuhi adalah $\tan x = -2 \, \, \, $ atau $ \tan x = -\frac{2}{1} $

Sehingga nilai :
$\sin x + \cos x = \frac{2}{\sqrt{5}} - \frac{1}{\sqrt{5}} = \frac{1}{\sqrt{5}} = \frac{1}{5} \sqrt{5} $
Jadi, nilai $\sin x + \cos x = \frac{1}{5} \sqrt{5} . \heartsuit$
$\begin{align*} 2\tan ^2 x + 3 \tan x - 2 & = 0 \\ (2\tan x -1)(\tan x + 2) & = 0 \\ \tan x = \frac{1}{2} & \vee \tan x = -2 \end{align*}$
Karena $x \, $ dikuadran II , maka nilai $\tan x \, \, $ harus negatif, sehingga yang memenuhi adalah $\tan x = -2 \, \, \, $ atau $ \tan x = -\frac{2}{1} $

Sehingga nilai :
$\sin x + \cos x = \frac{2}{\sqrt{5}} - \frac{1}{\sqrt{5}} = \frac{1}{\sqrt{5}} = \frac{1}{5} \sqrt{5} $
Jadi, nilai $\sin x + \cos x = \frac{1}{5} \sqrt{5} . \heartsuit$
Nomor 9
Pada $\Delta$ ABC diketahui D adalah titik tengah AC. Jika BC = $a $ , AC = $b $ , dan BD = $d $ , maka $d^2 = ....$
$\clubsuit \, $ Gambar
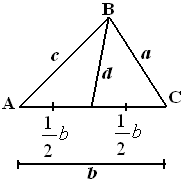
$\clubsuit \, $ Aturan cosinus pada segitiga ABD
$\begin{align*} d^2 & = c^2+(\frac{1}{2}b)^2 - 2. c.(\frac{1}{2}b) . \cos A \\ d^2 & = c^2+\frac{1}{4}b^2 - bc \cos A \, \, \, \text{...pers(i)} \end{align*}$
$\clubsuit \, $ Aturan cosinus pada segitiga ABC
$\begin{align*} a^2 & = b^2+c^2 - 2. b.c . \cos A \\ \cos A & = \frac{b^2+c^2-a^2}{2bc} \, \, \, \text{...pers(ii)} \end{align*}$
$\clubsuit \, $ Substitusi pers(ii) ke pers(i)
$\begin{align*} d^2 & = c^2+\frac{1}{4}b^2 - bc \cos A \, \, \, \text{...pers(i)} \\ d^2 & = c^2+\frac{1}{4}b^2 - bc .\frac{b^2+c^2-a^2}{2bc} \\ d^2 & = c^2+\frac{1}{4}b^2 - \frac{1}{2}b^2 - \frac{1}{2}c^2 + \frac{1}{2}a^2 \\ d^2 & = \frac{1}{2}a^2 + \frac{1}{2}c^2 - \frac{1}{4}b^2 \end{align*}$
Jadi, nilai $ d^2 = \frac{1}{2}a^2 + \frac{1}{2}c^2 - \frac{1}{4}b^2 . \heartsuit$

$\clubsuit \, $ Aturan cosinus pada segitiga ABD
$\begin{align*} d^2 & = c^2+(\frac{1}{2}b)^2 - 2. c.(\frac{1}{2}b) . \cos A \\ d^2 & = c^2+\frac{1}{4}b^2 - bc \cos A \, \, \, \text{...pers(i)} \end{align*}$
$\clubsuit \, $ Aturan cosinus pada segitiga ABC
$\begin{align*} a^2 & = b^2+c^2 - 2. b.c . \cos A \\ \cos A & = \frac{b^2+c^2-a^2}{2bc} \, \, \, \text{...pers(ii)} \end{align*}$
$\clubsuit \, $ Substitusi pers(ii) ke pers(i)
$\begin{align*} d^2 & = c^2+\frac{1}{4}b^2 - bc \cos A \, \, \, \text{...pers(i)} \\ d^2 & = c^2+\frac{1}{4}b^2 - bc .\frac{b^2+c^2-a^2}{2bc} \\ d^2 & = c^2+\frac{1}{4}b^2 - \frac{1}{2}b^2 - \frac{1}{2}c^2 + \frac{1}{2}a^2 \\ d^2 & = \frac{1}{2}a^2 + \frac{1}{2}c^2 - \frac{1}{4}b^2 \end{align*}$
Jadi, nilai $ d^2 = \frac{1}{2}a^2 + \frac{1}{2}c^2 - \frac{1}{4}b^2 . \heartsuit$
Nomor 10
$\displaystyle \lim_{ x \to -2} \frac{x^2+5x+6}{x^2-4} = .... $
$\spadesuit \, $ Memfaktorkan
$\begin{align} \displaystyle \lim_{ x \to -2} \frac{x^2+5x+6}{x^2-4} & = \displaystyle \lim_{ x \to -2} \frac{(x+2)(x+3)}{(x+2)(x-2)} \\ & = \displaystyle \lim_{ x \to -2} \frac{x+3}{x-2} \\ & = \frac{-2+3}{-2-2} \\ \displaystyle \lim_{ x \to -2} \frac{x^2+5x+6}{x^2-4} & = -\frac{1}{4} \end{align}$
Jadi, nilai limitnya adalah $ -\frac{1}{4} . \heartsuit $
$\begin{align} \displaystyle \lim_{ x \to -2} \frac{x^2+5x+6}{x^2-4} & = \displaystyle \lim_{ x \to -2} \frac{(x+2)(x+3)}{(x+2)(x-2)} \\ & = \displaystyle \lim_{ x \to -2} \frac{x+3}{x-2} \\ & = \frac{-2+3}{-2-2} \\ \displaystyle \lim_{ x \to -2} \frac{x^2+5x+6}{x^2-4} & = -\frac{1}{4} \end{align}$
Jadi, nilai limitnya adalah $ -\frac{1}{4} . \heartsuit $
Cara II
$\spadesuit \, $ Menggunakan turunan
$\begin{align} \displaystyle \lim_{ x \to -2} \frac{x^2+5x+6}{x^2-4} & = \displaystyle \lim_{ x \to -2} \frac{2x+5}{2x} \\ & = \frac{2.(-2)+5}{2.(-2)} \\ \displaystyle \lim_{ x \to -2} \frac{x^2+5x+6}{x^2-4} & = -\frac{1}{4} \end{align}$
Jadi, nilai limitnya adalah $ -\frac{1}{4} . \heartsuit $
$\spadesuit \, $ Menggunakan turunan
$\begin{align} \displaystyle \lim_{ x \to -2} \frac{x^2+5x+6}{x^2-4} & = \displaystyle \lim_{ x \to -2} \frac{2x+5}{2x} \\ & = \frac{2.(-2)+5}{2.(-2)} \\ \displaystyle \lim_{ x \to -2} \frac{x^2+5x+6}{x^2-4} & = -\frac{1}{4} \end{align}$
Jadi, nilai limitnya adalah $ -\frac{1}{4} . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.