Nomor 1
Penyelesaian pertidaksamaan $ \frac{x^2+x-6}{x-2} \geq 0 \, $ adalah ....
$\clubsuit \, $ Menentukan nilai $ x $
$\begin{align} \frac{x^2+x-6}{x-2} & \geq 0 \\ \frac{(x-2)(x+3)}{x-2} & \geq 0 \\ x = 2 \vee x = - 3 \end{align}$
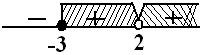
Jadi, solusinya adalah $ HP = \{ -3 \leq x < 2 \vee x > 2 \} . \heartsuit $
$\begin{align} \frac{x^2+x-6}{x-2} & \geq 0 \\ \frac{(x-2)(x+3)}{x-2} & \geq 0 \\ x = 2 \vee x = - 3 \end{align}$

Jadi, solusinya adalah $ HP = \{ -3 \leq x < 2 \vee x > 2 \} . \heartsuit $
Nomor 2
Deret aritmetika terdiri atas 10 suku dengan suku pertama 4 dan jumlah 10 suku pertamanya adalah 130. Suku yang terakhir deret
tersebut adalah ....
$\spadesuit \, $ Barisan aritmetika : $ U_n = a + (n-1)b \, $ dan $ \, S_n = \frac{n}{2} (2a+(n-1)b) $
$\spadesuit \, $ Menentukan nilai $ b \, $ dengan $ a = 4 $
$\begin{align} S_{10} & = 130 \\ \frac{10}{2} (2a+(10-1)b) & = 130 \\ 5(2.4 + 9b ) & = 130 \, \, \text{(bagi 5)} \\ 8 + 9b & = 26 \\ 9b & = 26 - 8 \\ 9b & = 18 \rightarrow b = 2 \end{align} $
$\spadesuit \, $ Menentukan suku terakhir ($U_{10}$)
$ U_{10} = a+9b = 4 + 9.2 = 4 + 18 = 22 $
Jadi, suku terakhirnya adalah 22. $ \heartsuit $
$\spadesuit \, $ Menentukan nilai $ b \, $ dengan $ a = 4 $
$\begin{align} S_{10} & = 130 \\ \frac{10}{2} (2a+(10-1)b) & = 130 \\ 5(2.4 + 9b ) & = 130 \, \, \text{(bagi 5)} \\ 8 + 9b & = 26 \\ 9b & = 26 - 8 \\ 9b & = 18 \rightarrow b = 2 \end{align} $
$\spadesuit \, $ Menentukan suku terakhir ($U_{10}$)
$ U_{10} = a+9b = 4 + 9.2 = 4 + 18 = 22 $
Jadi, suku terakhirnya adalah 22. $ \heartsuit $
Cara II
$\spadesuit \, $ Barisan aritmetika : $ \, S_n = \frac{n}{2} (a+U_n) $
$\spadesuit \, $ Menentukan suku terakhir ($U_{10}$)
$\begin{align} S_{10} & = 130 \\ \frac{10}{2} (a+U_{10}) & = 130 \\ 5(4+U_{10}) & = 130 \, \, \text{(bagi 5)} \\ 4 + U_{10} & = 26 \\ U_{10} & = 26-4 = 22 \end{align} $
Jadi, suku terakhirnya adalah 22. $ \heartsuit $
$\spadesuit \, $ Barisan aritmetika : $ \, S_n = \frac{n}{2} (a+U_n) $
$\spadesuit \, $ Menentukan suku terakhir ($U_{10}$)
$\begin{align} S_{10} & = 130 \\ \frac{10}{2} (a+U_{10}) & = 130 \\ 5(4+U_{10}) & = 130 \, \, \text{(bagi 5)} \\ 4 + U_{10} & = 26 \\ U_{10} & = 26-4 = 22 \end{align} $
Jadi, suku terakhirnya adalah 22. $ \heartsuit $
Nomor 3
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik A ke bidang BDE adalah ....
$\clubsuit \, $ Gambar

Panjang $ EP = \sqrt{AP^2+AE^2} = \sqrt{(3\sqrt{2})^2+6^2} = 3\sqrt{6} $
Jarak A ke BDE sama dengan jarak A ke EP yaitu panjang AM.
$\clubsuit \, $ Menentukan panjang AM dengan luas segitiga
$\begin{align} \text{Luas}_{\Delta AEP} \, \text{(alasnya AP)} & = \text{Luas}_{\Delta AEP} \text{(alasnya EP)} \\ \frac{1}{2} .AP.EA & = \frac{1}{2} . EP . AM \\ AP.EA & = EP . AM \\ AM & = \frac{AP.EA}{EP} \\ AM & = \frac{6.3\sqrt{2}}{3\sqrt{6}} \\ AM & = 2\sqrt{3} \end{align}$
Jadi, jarak A ke BDE adalah $ 2\sqrt{3} . \heartsuit $

Panjang $ EP = \sqrt{AP^2+AE^2} = \sqrt{(3\sqrt{2})^2+6^2} = 3\sqrt{6} $
Jarak A ke BDE sama dengan jarak A ke EP yaitu panjang AM.
$\clubsuit \, $ Menentukan panjang AM dengan luas segitiga
$\begin{align} \text{Luas}_{\Delta AEP} \, \text{(alasnya AP)} & = \text{Luas}_{\Delta AEP} \text{(alasnya EP)} \\ \frac{1}{2} .AP.EA & = \frac{1}{2} . EP . AM \\ AP.EA & = EP . AM \\ AM & = \frac{AP.EA}{EP} \\ AM & = \frac{6.3\sqrt{2}}{3\sqrt{6}} \\ AM & = 2\sqrt{3} \end{align}$
Jadi, jarak A ke BDE adalah $ 2\sqrt{3} . \heartsuit $
Cara II
$\clubsuit \, $ Gambar

Pada gambar di atas, terlihat bahwa AG dibagi menjadi tiga bagian yaitu AM, MK, dan KG , sehingga jarak A ke BDE sama dengan $ \frac{1}{3} AG $
$ AM = \frac{1}{3} AG = \frac{1}{3} . 6\sqrt{3} = 2\sqrt{3} $
Jadi, jarak A ke BDE adalah $ 2\sqrt{3} . \heartsuit $
$\clubsuit \, $ Gambar

Pada gambar di atas, terlihat bahwa AG dibagi menjadi tiga bagian yaitu AM, MK, dan KG , sehingga jarak A ke BDE sama dengan $ \frac{1}{3} AG $
$ AM = \frac{1}{3} AG = \frac{1}{3} . 6\sqrt{3} = 2\sqrt{3} $
Jadi, jarak A ke BDE adalah $ 2\sqrt{3} . \heartsuit $
Nomor 4
Bentuk sederhana $ \frac{\tan ^2 x + \cos ^2 x}{\sin x + \sec x } \, $ adalah ....
$\spadesuit \, $ Konsep dasar :
Identitas : $ \cos ^2 x = 1 - \sin ^2 x \, $ dan $ \, \tan ^2 x = \sec ^2 x - 1 $
Pemfaktoran : $ p^2 - q^2 = (p+q)(p-q) $
$\spadesuit \, $ Menyederhanakan soal
$\begin{align} \frac{\tan ^2 x + \cos ^2 x}{\sin x + \sec x } & = \frac{(\sec ^2 x - 1) + (1 - \sin ^2 x)}{(\sec x + \sin x )} \\ & = \frac{\sec ^2 x - \sin ^2 x}{(\sec x + \sin x )} \\ & = \frac{(\sec x + \sin x ).(\sec x - \sin x )}{(\sec x + \sin x )} \\ & = \sec x - \sin x \end{align}$
Jadi, bentuk sederhananya adalah $ \sec x - \sin x . \heartsuit $
Identitas : $ \cos ^2 x = 1 - \sin ^2 x \, $ dan $ \, \tan ^2 x = \sec ^2 x - 1 $
Pemfaktoran : $ p^2 - q^2 = (p+q)(p-q) $
$\spadesuit \, $ Menyederhanakan soal
$\begin{align} \frac{\tan ^2 x + \cos ^2 x}{\sin x + \sec x } & = \frac{(\sec ^2 x - 1) + (1 - \sin ^2 x)}{(\sec x + \sin x )} \\ & = \frac{\sec ^2 x - \sin ^2 x}{(\sec x + \sin x )} \\ & = \frac{(\sec x + \sin x ).(\sec x - \sin x )}{(\sec x + \sin x )} \\ & = \sec x - \sin x \end{align}$
Jadi, bentuk sederhananya adalah $ \sec x - \sin x . \heartsuit $
Nomor 5
Diketahui premis-premis :
* Jika saya minum kopi, saya tidak dapat tidur
* Saya tidur atau saya merasa pusing
* Saya minum kopi
Kesimpulan yang sah adalah ....
* Jika saya minum kopi, saya tidak dapat tidur
* Saya tidur atau saya merasa pusing
* Saya minum kopi
Kesimpulan yang sah adalah ....
$\clubsuit \, $ Menarik kesimpulan :
Silogisme : $\, \, \, \begin{array}{c} p \rightarrow q \\ q \rightarrow r \\ \hline \therefore \, p \rightarrow r \end{array} \, \, \, $ Modus ponens : $\, \, \, \begin{array}{c} p \rightarrow q \\ p \\ \hline \therefore q \end{array}$
$\clubsuit \, $ Mengubah premis-premis menjadi simbol matematika:
1). Jika $\underbrace{\text{saya minum kopi}}_{p}$, maka $\underbrace{\text{saya tidak dapat tidur}}_{\sim q}.$
ditulis : $p \rightarrow \sim q$
2). $\underbrace{\text{Saya tidur}}_{q} \, $ atau $\underbrace{\text{saya merasa pusing}}_{r}.$
ditulis : $q \vee r \, $ setara dengan $ \, \sim q \rightarrow r $
3). $\underbrace{\text{saya minum kopi}}_{p}$ . ditulis : $ p $
$\clubsuit \, $ Menarik kesimpulan dari premis-premis 1) , 2), dan 3):
Silogisme 1) dan 2): $\, \, \, \begin{array}{c} p \rightarrow \sim q \\ \sim q \rightarrow r \\ \hline \therefore \, p \rightarrow r \end{array} \, \, \, $ Modus ponens dengan 3): $\, \, \, \begin{array}{c} p \rightarrow r \\ p \\ \hline \therefore r \end{array}$
Jadi, kesimpulannya adalah $ r \, $ dibaca : saya merasa pusing. $\heartsuit$
Catatan : Tidak ada pilihan jawaban yang sesuai.
Silogisme : $\, \, \, \begin{array}{c} p \rightarrow q \\ q \rightarrow r \\ \hline \therefore \, p \rightarrow r \end{array} \, \, \, $ Modus ponens : $\, \, \, \begin{array}{c} p \rightarrow q \\ p \\ \hline \therefore q \end{array}$
$\clubsuit \, $ Mengubah premis-premis menjadi simbol matematika:
1). Jika $\underbrace{\text{saya minum kopi}}_{p}$, maka $\underbrace{\text{saya tidak dapat tidur}}_{\sim q}.$
ditulis : $p \rightarrow \sim q$
2). $\underbrace{\text{Saya tidur}}_{q} \, $ atau $\underbrace{\text{saya merasa pusing}}_{r}.$
ditulis : $q \vee r \, $ setara dengan $ \, \sim q \rightarrow r $
3). $\underbrace{\text{saya minum kopi}}_{p}$ . ditulis : $ p $
$\clubsuit \, $ Menarik kesimpulan dari premis-premis 1) , 2), dan 3):
Silogisme 1) dan 2): $\, \, \, \begin{array}{c} p \rightarrow \sim q \\ \sim q \rightarrow r \\ \hline \therefore \, p \rightarrow r \end{array} \, \, \, $ Modus ponens dengan 3): $\, \, \, \begin{array}{c} p \rightarrow r \\ p \\ \hline \therefore r \end{array}$
Jadi, kesimpulannya adalah $ r \, $ dibaca : saya merasa pusing. $\heartsuit$
Catatan : Tidak ada pilihan jawaban yang sesuai.
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.