Nomor 6
Agar sistem persamaan $\left\{ \begin{array}{c} 2x-y-1=0 \\ 4x-y-5=0 \\ ax-y-7=0 \end{array} \right. $
mempunyai penyelesaian , maka nilai $a$ adalah ...
mempunyai penyelesaian , maka nilai $a$ adalah ...
Nomor 7
Himpunan penyelesaian pertidaksamaan $\sqrt{x^2-2x} < \sqrt{3x+6} \, $ adalah ...
$\clubsuit \, $ Kuadratkan pertidaksamaan :
$\begin{align*} ( \sqrt{x^2-2x} )^2 & < ( \sqrt{3x+6} )^2 \\ x^2-2x & < 3x+6 \\ x^2-5x-6 & <0 \\ (x+1)(x-6)& =0 \\ x=-1 \, & \text{atau} \, x=6 \end{align*} $
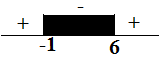
$HP_1=\{ -1 < x < 6 \} $
$\clubsuit \, $ Syarat bentuk akar :
$\sqrt{x^2-2x} \geq 0 \Leftrightarrow x^2-2x \geq 0 \Leftrightarrow x(x-2) \geq 0 \Leftrightarrow x=0 \, \text{atau} \, x=2 $

$HP_2=\{ x \leq 0 \, \text{atau} \, x\geq 2 \} $
$\sqrt{3x+6} \geq 0 \Leftrightarrow 3x+6 \geq 0 \Leftrightarrow x \geq -2 $
$HP_3=\{ x \geq -2 \} $
sehingga solusinya :
$ HP = HP_1 \cap HP_2 \cap HP_3 = \{ -1 < x \leq 0 \, \text{atau} \, 2 \leq x < 6 \} $
Jadi, $HP=\{ -1 < x \leq 0 \, \text{atau} \, 2 \leq x < 6 \} . \heartsuit$
$\begin{align*} ( \sqrt{x^2-2x} )^2 & < ( \sqrt{3x+6} )^2 \\ x^2-2x & < 3x+6 \\ x^2-5x-6 & <0 \\ (x+1)(x-6)& =0 \\ x=-1 \, & \text{atau} \, x=6 \end{align*} $
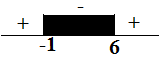
$HP_1=\{ -1 < x < 6 \} $
$\clubsuit \, $ Syarat bentuk akar :
$\sqrt{x^2-2x} \geq 0 \Leftrightarrow x^2-2x \geq 0 \Leftrightarrow x(x-2) \geq 0 \Leftrightarrow x=0 \, \text{atau} \, x=2 $

$HP_2=\{ x \leq 0 \, \text{atau} \, x\geq 2 \} $
$\sqrt{3x+6} \geq 0 \Leftrightarrow 3x+6 \geq 0 \Leftrightarrow x \geq -2 $
$HP_3=\{ x \geq -2 \} $
sehingga solusinya :
$ HP = HP_1 \cap HP_2 \cap HP_3 = \{ -1 < x \leq 0 \, \text{atau} \, 2 \leq x < 6 \} $
Jadi, $HP=\{ -1 < x \leq 0 \, \text{atau} \, 2 \leq x < 6 \} . \heartsuit$
Cara II : Metode Suka (substitusi angka)
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=1 \Rightarrow \sqrt{x^2-2x} & < \sqrt{3x+6} \\ \sqrt{1^2-2.1} & < \sqrt{3.1+6} \\ \sqrt{-1} & < \sqrt{9} \, \, \text{(pasti salah)} \end{align*}$
yang ada $x=1$ salah, opsi yang salah adalah A dan C.
$\begin{align*} \text{Pilih} \, x=-1 \Rightarrow \sqrt{x^2-2x} & < \sqrt{3x+6} \\ \sqrt{(-1)^2-2.(-1)} & < \sqrt{3.(-1)+6} \\ \sqrt{5} & < \sqrt{3} \, \, \text{(salah)} \end{align*}$
yang ada $x=-1$ salah, opsi yang salah adalah B dan D.
Jadi, opsi yang benar adalah E yaitu
$HP=\{ -1 < x \leq 0 \, \text{atau} \, 2 \leq x < 6 \} . \heartsuit$
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=1 \Rightarrow \sqrt{x^2-2x} & < \sqrt{3x+6} \\ \sqrt{1^2-2.1} & < \sqrt{3.1+6} \\ \sqrt{-1} & < \sqrt{9} \, \, \text{(pasti salah)} \end{align*}$
yang ada $x=1$ salah, opsi yang salah adalah A dan C.
$\begin{align*} \text{Pilih} \, x=-1 \Rightarrow \sqrt{x^2-2x} & < \sqrt{3x+6} \\ \sqrt{(-1)^2-2.(-1)} & < \sqrt{3.(-1)+6} \\ \sqrt{5} & < \sqrt{3} \, \, \text{(salah)} \end{align*}$
yang ada $x=-1$ salah, opsi yang salah adalah B dan D.
Jadi, opsi yang benar adalah E yaitu
$HP=\{ -1 < x \leq 0 \, \text{atau} \, 2 \leq x < 6 \} . \heartsuit$
Nomor 8
Jika $\cos x=2\sin x$ , maka nilai $\sin x \cos x$ adalah ...
$\spadesuit \, $ Menentukan nilai $\tan x$ dengan $\tan x=\frac{\sin x}{\cos x}$ :
$\cos x=2\sin x \Leftrightarrow \frac{\sin x}{\cos x}=\frac{1}{2} \Leftrightarrow \tan x=\frac{1}{2}$
$\spadesuit \, $ Buat segitiga dari nilai $\tan x=\frac{1}{2}$ :
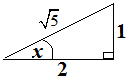
sehingga $\sin x \cos x=\frac{1}{\sqrt{5}}.\frac{2}{\sqrt{5}}=\frac{2}{5}$
Jadi, nilai $ \sin x \cos x=\frac{2}{5}. \, \heartsuit $
$\cos x=2\sin x \Leftrightarrow \frac{\sin x}{\cos x}=\frac{1}{2} \Leftrightarrow \tan x=\frac{1}{2}$
$\spadesuit \, $ Buat segitiga dari nilai $\tan x=\frac{1}{2}$ :

sehingga $\sin x \cos x=\frac{1}{\sqrt{5}}.\frac{2}{\sqrt{5}}=\frac{2}{5}$
Jadi, nilai $ \sin x \cos x=\frac{2}{5}. \, \heartsuit $
Nomor 9
Jumlah suku ke-4 dan suku ke-5 dari suatu barisan aritmetika adalah 55, sedangkan suku ke-9 dikurangi dua kali suku ke-2 bernilai 1.
Jumlah tiga suku pertama barisan tersebut adalah ...
$\clubsuit \, $ Barisan aritmatika : $u_n=a+(n-1)b \, \, $ dan $\, s_n=\frac{n}{2}(2a+(n-1)b)$
$u_4+u_5=55 \Rightarrow (a+3b)+(a+4b)=55 \Rightarrow 2a+7b=55 \, \text{...pes(i)} $
$u_9-2u_2=1 \Rightarrow (a+8b)-2(a+b)=1 \Rightarrow -a+6b=1 \, \text{...pes(ii)} $
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii) , diperoleh $a=17$ dan $b=3$
$\clubsuit \, $ Jumlah 3 suku pertama ($s_3$) :
$s_3=\frac{3}{2}(2a+(3-1)b) \Rightarrow s_3=\frac{3}{2}(2.17+2.3) \Rightarrow s_3= 60$
Jadi, Jumlah 3 suku pertama adalah 60. $\heartsuit $
$u_4+u_5=55 \Rightarrow (a+3b)+(a+4b)=55 \Rightarrow 2a+7b=55 \, \text{...pes(i)} $
$u_9-2u_2=1 \Rightarrow (a+8b)-2(a+b)=1 \Rightarrow -a+6b=1 \, \text{...pes(ii)} $
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii) , diperoleh $a=17$ dan $b=3$
$\clubsuit \, $ Jumlah 3 suku pertama ($s_3$) :
$s_3=\frac{3}{2}(2a+(3-1)b) \Rightarrow s_3=\frac{3}{2}(2.17+2.3) \Rightarrow s_3= 60$
Jadi, Jumlah 3 suku pertama adalah 60. $\heartsuit $
Nomor 10
Jika $\left( \begin{matrix} y \\ x \end{matrix} \right) =\left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right)^{-1}\left( \begin{matrix} 4 \\ -1 \end{matrix} \right) \,$
dengan $x\neq -\frac{1}{2}$, maka nilai $\frac{1}{2}x+y=...$
$\spadesuit \, $ Kedua ruas dikalikan dengan matriks $\left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right)$
dan gunakan sifat $A.A^{-1}=I$ serta $ I.B=B$
$\begin{align*} \left( \begin{matrix} y \\ x \end{matrix} \right) &=\left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right)^{-1}\left( \begin{matrix} 4 \\ -1 \end{matrix} \right) \\ \left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right) .\left( \begin{matrix} y \\ x \end{matrix} \right) &=\left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right) .\left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right)^{-1}\left( \begin{matrix} 4 \\ -1 \end{matrix} \right) \\ \left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right) .\left( \begin{matrix} y \\ x \end{matrix} \right) &=I.\left( \begin{matrix} 4 \\ -1 \end{matrix} \right) \\ \left( \begin{matrix} x+2y \\ x^2-y \end{matrix} \right) & = \left( \begin{matrix} 4 \\ -1 \end{matrix} \right) \\ \text{sehingga} \, \, x+2y & = 4 \end{align*}$
$\spadesuit \, $ Menentukan nilai $\frac{1}{2}x+y$
$\begin{align*} x+2y & = 4 \, \, \text{(bagi 2 kedua ruas)} \\ \frac{1}{2}x+y & = 2 \end{align*}$
Jadi, nilai $\frac{1}{2}x+y=2. \heartsuit $
dan gunakan sifat $A.A^{-1}=I$ serta $ I.B=B$
$\begin{align*} \left( \begin{matrix} y \\ x \end{matrix} \right) &=\left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right)^{-1}\left( \begin{matrix} 4 \\ -1 \end{matrix} \right) \\ \left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right) .\left( \begin{matrix} y \\ x \end{matrix} \right) &=\left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right) .\left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right)^{-1}\left( \begin{matrix} 4 \\ -1 \end{matrix} \right) \\ \left( \begin{matrix} 2 & 1 \\ -1 & x \end{matrix} \right) .\left( \begin{matrix} y \\ x \end{matrix} \right) &=I.\left( \begin{matrix} 4 \\ -1 \end{matrix} \right) \\ \left( \begin{matrix} x+2y \\ x^2-y \end{matrix} \right) & = \left( \begin{matrix} 4 \\ -1 \end{matrix} \right) \\ \text{sehingga} \, \, x+2y & = 4 \end{align*}$
$\spadesuit \, $ Menentukan nilai $\frac{1}{2}x+y$
$\begin{align*} x+2y & = 4 \, \, \text{(bagi 2 kedua ruas)} \\ \frac{1}{2}x+y & = 2 \end{align*}$
Jadi, nilai $\frac{1}{2}x+y=2. \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.