Nomor 11
Empat koin palsu dicampur dengan delapan koin asli. Jika dua koin diambil secara acak, maka peluang terambil satu koin asli dan satu
koin palsu adalah ...
$\spadesuit \, $ Ada 4 koin palsu dan 8 koin asli (4p8a) , diambil 2 koin :
$n(S)=C_2^12=66$
$\spadesuit \, $ Kejadian yang diharapkan (K) terambil 1p1a
$n(K)=C_1^4.C_1^8=4.8=32$
$\spadesuit \, $ Peluangnya:
$P(K)=\frac{n(K)}{n(S)}=\frac{32}{66}=\frac{16}{33}$
Jadi, peluang terambil 1 koin palsu dan 1 koin asli adalah $\frac{16}{33}. \heartsuit $
$n(S)=C_2^12=66$
$\spadesuit \, $ Kejadian yang diharapkan (K) terambil 1p1a
$n(K)=C_1^4.C_1^8=4.8=32$
$\spadesuit \, $ Peluangnya:
$P(K)=\frac{n(K)}{n(S)}=\frac{32}{66}=\frac{16}{33}$
Jadi, peluang terambil 1 koin palsu dan 1 koin asli adalah $\frac{16}{33}. \heartsuit $
Nomor 12
Jika $f(x)=\frac{x+1}{x-1}, \, x\neq 1 $ , maka $f^{-1} \left( \frac{1}{x} \right) =...$
$\clubsuit \, $ invers dari $f(x)=\frac{ax+b}{cx+d} \Rightarrow f^{-1}(x)=\frac{-dx+b}{cx-a} $:
$\begin{align*} f(x)=\frac{x+1}{x-1} \Rightarrow f^{-1}(x) = \frac{x+1}{x-1} \end{align*}$
$\clubsuit \, $ Menentukan $ f^{-1} \left( \frac{1}{x} \right) $
$\begin{align*} f^{-1} \left( \frac{1}{x} \right) & = \frac{ \left( \frac{1}{x} \right) +1}{ \left( \frac{1}{x} \right) -1} \\ &= \frac{ \left( \frac{1}{x} \right) +1}{ \left( \frac{1}{x} \right) -1} . \frac{x}{x} \\ &= \frac{1+x}{1-x} = -\frac{x+1}{x-1} \\ f^{-1} \left( \frac{1}{x} \right) &= -f(x) \end{align*}$
Jadi, $ f^{-1} \left( \frac{1}{x} \right) = - f(x) . \heartsuit $
$\begin{align*} f(x)=\frac{x+1}{x-1} \Rightarrow f^{-1}(x) = \frac{x+1}{x-1} \end{align*}$
$\clubsuit \, $ Menentukan $ f^{-1} \left( \frac{1}{x} \right) $
$\begin{align*} f^{-1} \left( \frac{1}{x} \right) & = \frac{ \left( \frac{1}{x} \right) +1}{ \left( \frac{1}{x} \right) -1} \\ &= \frac{ \left( \frac{1}{x} \right) +1}{ \left( \frac{1}{x} \right) -1} . \frac{x}{x} \\ &= \frac{1+x}{1-x} = -\frac{x+1}{x-1} \\ f^{-1} \left( \frac{1}{x} \right) &= -f(x) \end{align*}$
Jadi, $ f^{-1} \left( \frac{1}{x} \right) = - f(x) . \heartsuit $
Nomor 13
Garis $l$ mempunyai gradien 2. Jika $l$ menyinggung grafik fungsi $f(x)=-x^2+px+1$ di $x=1$ , maka persamaan $l$ adalah ...
$\spadesuit \, $ Garis $l$ gradiennya $m_l=2$
$\spadesuit \, $ Gradien garis singgung di $x=1$
$f(x)=-x^2+px+1 \Rightarrow f^\prime (x) = -2x+p$
gradien : $m_l=f^\prime (1) \Rightarrow 2=-2.1+p \Rightarrow p=4$
fungsinya : $f(x)=-x^2+4x+1$
$\spadesuit \, $ Menentukan titik singgung dengan $x=1$
$x=1 \Rightarrow y=-1^2+4.1+1=4 $
titik singgungnya : (1,4)
$\spadesuit \, $ persamaan garis singgung $l$ di titik (1,4) dengan $m=2$
$\begin{align*} y-y_1&=m(x-x_1) \\ y-4&=2(x-1) \\ y&=2x+2 \end{align*}$
Jadi, PGS nya adalah $y=2x+2 . \heartsuit $
$\spadesuit \, $ Gradien garis singgung di $x=1$
$f(x)=-x^2+px+1 \Rightarrow f^\prime (x) = -2x+p$
gradien : $m_l=f^\prime (1) \Rightarrow 2=-2.1+p \Rightarrow p=4$
fungsinya : $f(x)=-x^2+4x+1$
$\spadesuit \, $ Menentukan titik singgung dengan $x=1$
$x=1 \Rightarrow y=-1^2+4.1+1=4 $
titik singgungnya : (1,4)
$\spadesuit \, $ persamaan garis singgung $l$ di titik (1,4) dengan $m=2$
$\begin{align*} y-y_1&=m(x-x_1) \\ y-4&=2(x-1) \\ y&=2x+2 \end{align*}$
Jadi, PGS nya adalah $y=2x+2 . \heartsuit $
$\clubsuit \, $ Permisalan: $p=2^x$
$\begin{align*} 2^{2x+2}-17(2^x)+4 & <0 \\ 2^2.2^{2x}-17(2^x)+4 & <0 \\ 4(2^x)^2-17(2^x)+4 & <0 \\ 4p^2-17p+4 & < 0 \\ (4p-1)(p-4) & = 0 \\ p=\frac{1}{4} \, & \text{atau} \, p=4 \\ p=\frac{1}{4} & \Rightarrow 2^x=\frac{1}{4} \Rightarrow 2^x = 2^{-2} \Rightarrow x=-2 \\ p=4 & \Rightarrow 2^x=4 \Rightarrow 2^x = 2^2 \Rightarrow x=2 \end{align*} $
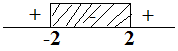
Jadi, $HP = \{ -2 < x < 2 \} . \heartsuit $
$\begin{align*} 2^{2x+2}-17(2^x)+4 & <0 \\ 2^2.2^{2x}-17(2^x)+4 & <0 \\ 4(2^x)^2-17(2^x)+4 & <0 \\ 4p^2-17p+4 & < 0 \\ (4p-1)(p-4) & = 0 \\ p=\frac{1}{4} \, & \text{atau} \, p=4 \\ p=\frac{1}{4} & \Rightarrow 2^x=\frac{1}{4} \Rightarrow 2^x = 2^{-2} \Rightarrow x=-2 \\ p=4 & \Rightarrow 2^x=4 \Rightarrow 2^x = 2^2 \Rightarrow x=2 \end{align*} $

Jadi, $HP = \{ -2 < x < 2 \} . \heartsuit $
$\clubsuit \, $ Cara II : Metode Suka (substitusi angka)
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=0 \Rightarrow 2^{2.0+2}-17(2^0)+4 & < 0 \\ 4-17+4 & < 0 \\ -9 & < 0 \, \, \text{(benar)} \end{align*}$
yang ada $x=0$ benar, opsi yang salah adalah A, B dan D.
$\begin{align*} \text{Pilih} \, x=-1 \Rightarrow 2^{2.(-1)+2}-17(2^{-1})+4 & < 0 \\ 1- \frac{17}{2} +4 & < 0 \\ -\frac{7}{2} & < 0 \, \, \text{(benar)} \end{align*}$
yang ada $x=-1$ benar, opsi yang salah adalah C.
Jadi, opsi yang benar adalah E yaitu
$HP=\{ -2 < x < 2 \} . \heartsuit$
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=0 \Rightarrow 2^{2.0+2}-17(2^0)+4 & < 0 \\ 4-17+4 & < 0 \\ -9 & < 0 \, \, \text{(benar)} \end{align*}$
yang ada $x=0$ benar, opsi yang salah adalah A, B dan D.
$\begin{align*} \text{Pilih} \, x=-1 \Rightarrow 2^{2.(-1)+2}-17(2^{-1})+4 & < 0 \\ 1- \frac{17}{2} +4 & < 0 \\ -\frac{7}{2} & < 0 \, \, \text{(benar)} \end{align*}$
yang ada $x=-1$ benar, opsi yang salah adalah C.
Jadi, opsi yang benar adalah E yaitu
$HP=\{ -2 < x < 2 \} . \heartsuit$
Nomor 15
Diketahui $x_1$ dan $x_2$ akar-akar real persamaan $x^2+3x+p=0$, dengan $x_1$ dan $x_2$ kedua-duanya tidak sama dengan nol. Jika $x_1+x_2$,
$x_1x_2$, dan $x_1^2x_2^2$ merupakan 3 suku pertama barisan aritmetika , maka $p=...$
$\clubsuit \, $ Menentukan jumlah dan kali akar-akarnya:
$x_1+x_2=\frac{-b}{a}=\frac{-3}{1}=-3 \, \, $ dan $\, \, x_1.x_2=\frac{c}{a}=\frac{p}{1}=p$
$\clubsuit \, $ Barisan aritmatika $x_1+x_2$, $x_1x_2$, dan $x_1^2x_2^2$ memiliki beda sama :
$x_1x_2 - (x_1+x_2) = x_1^2x_2^2 - x_1x_2 \Rightarrow 2(x_1x_2)= (x_1+x_2) + (x_1.x_2)^2 $
$\clubsuit \, $ Menentukan nilai $p$
$\begin{align*} 2(x_1x_2) & = (x_1+x_2) + (x_1.x_2)^2 \\ 2. p & = -3 + (p)^2 \\ p^2-2p-3 &= 0 \\ (p+1)(p-3) & = 0 \\ p=-1 \, & \text{atau} \, p=3 \end{align*} $
$\clubsuit \, $ Cek nilai $p$ yang memenuhi :
$\begin{align*} p=3 \Rightarrow x^2+3x+p&=0 \\ x^2+3x+3&=0 \\ D&=b^2-4ac \\ &=3^2-4.1.3=-3 < 0 \\ D & < 0 \end{align*} $
Karena $D<0$ , maka akar-akar nya tidak real.
sehingga $p=-1$ yang memenuhi .
Jadi, nilai $p=-1. \heartsuit $
$x_1+x_2=\frac{-b}{a}=\frac{-3}{1}=-3 \, \, $ dan $\, \, x_1.x_2=\frac{c}{a}=\frac{p}{1}=p$
$\clubsuit \, $ Barisan aritmatika $x_1+x_2$, $x_1x_2$, dan $x_1^2x_2^2$ memiliki beda sama :
$x_1x_2 - (x_1+x_2) = x_1^2x_2^2 - x_1x_2 \Rightarrow 2(x_1x_2)= (x_1+x_2) + (x_1.x_2)^2 $
$\clubsuit \, $ Menentukan nilai $p$
$\begin{align*} 2(x_1x_2) & = (x_1+x_2) + (x_1.x_2)^2 \\ 2. p & = -3 + (p)^2 \\ p^2-2p-3 &= 0 \\ (p+1)(p-3) & = 0 \\ p=-1 \, & \text{atau} \, p=3 \end{align*} $
$\clubsuit \, $ Cek nilai $p$ yang memenuhi :
$\begin{align*} p=3 \Rightarrow x^2+3x+p&=0 \\ x^2+3x+3&=0 \\ D&=b^2-4ac \\ &=3^2-4.1.3=-3 < 0 \\ D & < 0 \end{align*} $
Karena $D<0$ , maka akar-akar nya tidak real.
sehingga $p=-1$ yang memenuhi .
Jadi, nilai $p=-1. \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.