Nomor 1
Jika $1+\frac{6}{x}+\frac{9}{x^2}=0 $ , maka $\frac{3}{x} $ adalah ...
$\clubsuit \, $ Menentukan nilai $x$
$\begin{align} 1+\frac{6}{x}+\frac{9}{x^2} & = 0 \, \, \text{(kali } \, x^2 ) \\ x^2 + 6x + 0 & = 0 \\ (x+3)^2 & = 0 \\ x & = -3 \end{align}$
$\clubsuit \, $ Menentukan nilai $\frac{3}{x}$
$\frac{3}{x} = \frac{3}{-3} = -1 $
Jadi, nilai $\frac{3}{x} = -1 .\heartsuit $
$\begin{align} 1+\frac{6}{x}+\frac{9}{x^2} & = 0 \, \, \text{(kali } \, x^2 ) \\ x^2 + 6x + 0 & = 0 \\ (x+3)^2 & = 0 \\ x & = -3 \end{align}$
$\clubsuit \, $ Menentukan nilai $\frac{3}{x}$
$\frac{3}{x} = \frac{3}{-3} = -1 $
Jadi, nilai $\frac{3}{x} = -1 .\heartsuit $
Nomor 2
Pernyataan yang setara (ekivalen) dengan $|4x-5| < 13 $ adalah ...
$\spadesuit \, $ Rumus Dasar : $|f(x)| < a \Rightarrow -a < f(x) < a $
$\begin{align} |4x-5| & < 13 \\ -13 < & 4x-5 < 13 \, \, \text{(tambah 5)} \\ -13 + 5 < & 4x-5 + 5 < 13 + 5 \\ -8 < & 4x < 18 \, \, \text{(bagi 4)} \\ \frac{-8}{4} < & \frac{4x}{4} < \frac{18}{4} \\ -2 < & x < \frac{9}{2} \, \, \text{(kali 6)} \\ -12 < & 6x < 27 \end{align}$
Jadi, setara dengan $ -12 < 6x < 27 . \heartsuit $
$\begin{align} |4x-5| & < 13 \\ -13 < & 4x-5 < 13 \, \, \text{(tambah 5)} \\ -13 + 5 < & 4x-5 + 5 < 13 + 5 \\ -8 < & 4x < 18 \, \, \text{(bagi 4)} \\ \frac{-8}{4} < & \frac{4x}{4} < \frac{18}{4} \\ -2 < & x < \frac{9}{2} \, \, \text{(kali 6)} \\ -12 < & 6x < 27 \end{align}$
Jadi, setara dengan $ -12 < 6x < 27 . \heartsuit $
Nomor 3
Satuan ukuran televisi adalah inci yang diukur pada diagonal layarnya. Jika panjang layar dibanding lebarnya adalah 4 : 3,
maka televisi berukuran 30 inci memiliki panjang horizontal ...
$\clubsuit \, $ Perbandingannya :
$\frac{p}{l}=\frac{4x}{3x} \Rightarrow \text{artinya} \, p=4x \, \text{dan} \, l=3x$
$\clubsuit \, $ Menentukan nilai $x$
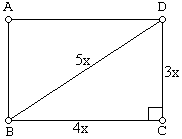
Diagonal layarnya 30.
$5x = 30 \rightarrow x = 6 $
Sehingga panjangnya : $4x = 4 \times 6 = 24 $
Jadi, panjangnya adalah 24 inci. $ \heartsuit $
$\frac{p}{l}=\frac{4x}{3x} \Rightarrow \text{artinya} \, p=4x \, \text{dan} \, l=3x$
$\clubsuit \, $ Menentukan nilai $x$

Diagonal layarnya 30.
$5x = 30 \rightarrow x = 6 $
Sehingga panjangnya : $4x = 4 \times 6 = 24 $
Jadi, panjangnya adalah 24 inci. $ \heartsuit $
Nomor 4
Jumlah 101 bilangan genap berurutan adalah 13130. Jumlah 3 bilangan terkecil yang pertama dari bilangan-bilangan genap itu adalah ...
$\spadesuit \, $ Rumus dasar : $S_n = \frac{n}{2}(2a+(n-1)b) $
$\spadesuit \, $ Menentukan nilai $a$ (suku pertamanya)
Barisan bilangan genap, nilai bedanya = 2.
$\begin{align*} S_{101} & = \frac{101}{2}(2a+(101-1).2) \\ 13130 & = \frac{101}{\not{2}}(\not{2}a+100.\not{2}) \\ 13130 & = 101(a+100) \\ 130 & = a + 100 \\ a & = 30 \end{align*}$
$\spadesuit \, $ Jumlah 3 suku pertama
$\begin{align*} S_{3} & = \frac{3}{2}(2a+(3-1).2) \\ & = \frac{3}{\not{2}}(\not{2}.30+2.\not{2}) \\ & = 3.(30+2) \\ & = 96 \end{align*}$
Jadi, jumlah 3 suku pertamanya adalah 96. $ \heartsuit$
$\spadesuit \, $ Menentukan nilai $a$ (suku pertamanya)
Barisan bilangan genap, nilai bedanya = 2.
$\begin{align*} S_{101} & = \frac{101}{2}(2a+(101-1).2) \\ 13130 & = \frac{101}{\not{2}}(\not{2}a+100.\not{2}) \\ 13130 & = 101(a+100) \\ 130 & = a + 100 \\ a & = 30 \end{align*}$
$\spadesuit \, $ Jumlah 3 suku pertama
$\begin{align*} S_{3} & = \frac{3}{2}(2a+(3-1).2) \\ & = \frac{3}{\not{2}}(\not{2}.30+2.\not{2}) \\ & = 3.(30+2) \\ & = 96 \end{align*}$
Jadi, jumlah 3 suku pertamanya adalah 96. $ \heartsuit$
Nomor 5
Diketahui $f(x)=(x-a)(x-b) $ dengan $a$ , $b$, dan $x$ bilangan real dan $a < b $ . Pernyataan berikut yang benar adalah ...
$\clubsuit \, $ Menyederhanakan fungsi dan sketsa gambarnya
$f(x)=(x-a)(x-b) = x^2 - (a+b)x+ab $
karena koefisien $x^2$ positif ($a>0$) , maka kurva terbuka ke atas dengan titik potong sumbu X di $x=a$ dan $x=b$

Catatan :
* karena $a < b $ , maka letak $a$ selalu di kiri $b$ .
* Nilai $a$ dan $b$ bisa positif juga negatif, sehingga sketsanya ada berbagai macam berikut ini

$\clubsuit \, $ Analisa grafiknya
Untuk interval $x$ atara $a$ dan $b$ , maka nilai fungsinya negatif (kurva ada di bawah sumbu X).
Sehingga disimpulkan :
jika $ a < x < b$ , maka $f(x) < 0 $ dan jika $x < a $ atau $x > b $ , maka $ f(x) > 0 $
Jadi, jika $ a < x < b$ , maka $f(x) < 0 . \heartsuit$
$f(x)=(x-a)(x-b) = x^2 - (a+b)x+ab $
karena koefisien $x^2$ positif ($a>0$) , maka kurva terbuka ke atas dengan titik potong sumbu X di $x=a$ dan $x=b$

Catatan :
* karena $a < b $ , maka letak $a$ selalu di kiri $b$ .
* Nilai $a$ dan $b$ bisa positif juga negatif, sehingga sketsanya ada berbagai macam berikut ini

$\clubsuit \, $ Analisa grafiknya
Untuk interval $x$ atara $a$ dan $b$ , maka nilai fungsinya negatif (kurva ada di bawah sumbu X).
Sehingga disimpulkan :
jika $ a < x < b$ , maka $f(x) < 0 $ dan jika $x < a $ atau $x > b $ , maka $ f(x) > 0 $
Jadi, jika $ a < x < b$ , maka $f(x) < 0 . \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.