Nomor 1
Nilai $x \, $ yang menyebabkan pernyataan :
" Jika $x^2 + x = 6 \, $ , maka $ \, x^2 + 3x < 9 \, $ "
Bernilai salah adalah ....
" Jika $x^2 + x = 6 \, $ , maka $ \, x^2 + 3x < 9 \, $ "
Bernilai salah adalah ....
$\clubsuit \, $ Menentukan nilai $ \, x $
$x^2+x=6 \leftrightarrow x^2+x-6=0 \leftrightarrow (x-2)(x+3)=0 \leftrightarrow x=2 \vee x=-3 $
$\clubsuit \, $ Cek kebenaran
$\begin{align} x=2 \rightarrow x^2+3x & < 9 \\ 2^2+3.2 & < 9 \\ 10 & < 9 \, \, \, \text{(salah)} \end{align}$
$\begin{align} x=-3 \rightarrow x^2+3x & < 9 \\ (-3)^2+3.(-3) & < 9 \\ 0 & < 9 \, \, \, \text{(benar)} \end{align}$
$\clubsuit \, $ Pernyataan " Jika P, maka Q" bernilai salah jika P benar dan Q salah.
Sehingga " Jika $x^2 + x = 6 \, $ , maka $ \, x^2 + 3x < 9 \, $ " bernilai salah untuk $ \, x=2$
Jadi, pernyataan SALAH untuk $ \, x=2 . \heartsuit $
$x^2+x=6 \leftrightarrow x^2+x-6=0 \leftrightarrow (x-2)(x+3)=0 \leftrightarrow x=2 \vee x=-3 $
$\clubsuit \, $ Cek kebenaran
$\begin{align} x=2 \rightarrow x^2+3x & < 9 \\ 2^2+3.2 & < 9 \\ 10 & < 9 \, \, \, \text{(salah)} \end{align}$
$\begin{align} x=-3 \rightarrow x^2+3x & < 9 \\ (-3)^2+3.(-3) & < 9 \\ 0 & < 9 \, \, \, \text{(benar)} \end{align}$
$\clubsuit \, $ Pernyataan " Jika P, maka Q" bernilai salah jika P benar dan Q salah.
Sehingga " Jika $x^2 + x = 6 \, $ , maka $ \, x^2 + 3x < 9 \, $ " bernilai salah untuk $ \, x=2$
Jadi, pernyataan SALAH untuk $ \, x=2 . \heartsuit $
Nomor 2
Agar ketiga garis $ 3x-y+1 = 0; \, 2x-y-3=0; \, $ dan $ \, x-ay-7 =0 \, $ berpotongan pada suatu titik, maka $ a \, $ harus bernilai ....
$\spadesuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} 3x-y+1 = 0 & \\ 2x-y-3=0 & - \\ \hline x = -4 & \end{array} $
pers(ii): $ 2x-y-3=0 \rightarrow 2.(-4)-y-3=0 \rightarrow y = -11 $
sehingga titik potongnya adalah (-4, -11)
$\spadesuit \, $ Substitusi titik potong ke pers(iii)
$x-ay-7 =0 \rightarrow (-4)-a.(-11)-7 =0 \rightarrow a = 1 $
Jadi, nilai $ a = 1. \heartsuit $
$\begin{array}{cc} 3x-y+1 = 0 & \\ 2x-y-3=0 & - \\ \hline x = -4 & \end{array} $
pers(ii): $ 2x-y-3=0 \rightarrow 2.(-4)-y-3=0 \rightarrow y = -11 $
sehingga titik potongnya adalah (-4, -11)
$\spadesuit \, $ Substitusi titik potong ke pers(iii)
$x-ay-7 =0 \rightarrow (-4)-a.(-11)-7 =0 \rightarrow a = 1 $
Jadi, nilai $ a = 1. \heartsuit $
Nomor 3
Misalkan $ f(x) = \left\{ \begin{array}{cc}
2x-1, & \text{untuk} \, \, \, \, 0 < x < 1 \\
x^2+1, & \text{untuk} \, \, x \, \, \text{yang lain}
\end{array} \right. $
maka $ f(2)f(-4)+f\left( \frac{1}{2} \right) f(3) = .... $
maka $ f(2)f(-4)+f\left( \frac{1}{2} \right) f(3) = .... $
$\clubsuit \, $ Fungsi $f(x)$ berlaku sesuai nilai $x$ yang disubstitusikan
$\clubsuit \, $ Menentukan nilai fungsi
$\begin{align} x = 2 \rightarrow f(x) & = x^2 + 1 \\ f(2) & = 2^2 + 1 = 5 \\ x = -4 \rightarrow f(x) & = x^2 + 1 \\ f(-4) & = (-4)^2 + 1 = 17 \\ x = \frac{1}{2} \rightarrow f(x) & = 2x - 1 \\ f(\frac{1}{2}) & = 2.(\frac{1}{2}) - 1 = 0 \\ x = 3 \rightarrow f(x) & = x^2 + 1 \\ f(3) & = (3)^2 + 1 = 10 \end{align}$
$ \clubsuit \, $ Menentukan hasilnya
$f(2).f(-4)+f(\frac{1}{2}).f(3) = 5.17 + 0 . 10 = 85 $
Jadi, hasilnya adalah 85. $ \heartsuit $
$\clubsuit \, $ Menentukan nilai fungsi
$\begin{align} x = 2 \rightarrow f(x) & = x^2 + 1 \\ f(2) & = 2^2 + 1 = 5 \\ x = -4 \rightarrow f(x) & = x^2 + 1 \\ f(-4) & = (-4)^2 + 1 = 17 \\ x = \frac{1}{2} \rightarrow f(x) & = 2x - 1 \\ f(\frac{1}{2}) & = 2.(\frac{1}{2}) - 1 = 0 \\ x = 3 \rightarrow f(x) & = x^2 + 1 \\ f(3) & = (3)^2 + 1 = 10 \end{align}$
$ \clubsuit \, $ Menentukan hasilnya
$f(2).f(-4)+f(\frac{1}{2}).f(3) = 5.17 + 0 . 10 = 85 $
Jadi, hasilnya adalah 85. $ \heartsuit $
Nomor 4
Garis yang sejajar dengan garis $2x+y=15 \, $ memotong kurva $ y = 6 + x - x^2 \, $ di titik (4, -6) dan ....
$\spadesuit \, $ Gambar
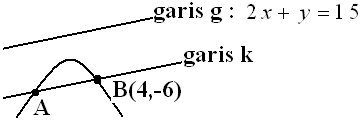
$\spadesuit \, $ Gradien garis g
$2x+y=15 \rightarrow m_g = \frac{-a}{b} = \frac{-2}{1} = -2 $
Garis k sejajar dengan garis g, sehingga gradiennya sama : $ m_k = m_g = -2 $
$\spadesuit \, $ Persamaan garis k
$y-y_1 = m(x-x_1) \rightarrow y-(-6) = -2(x-4) \rightarrow y = -2x + 2 $
$\spadesuit \, $ Menentukan titik potong garis k dan parabola
$\begin{align} y_1 & = y_2 \\ -2x+2 & = 6+x-x^2 \\ x^2-3x-4 & = 0 \\ (x+1)(x-4) & = 0 \\ x=-1 & \vee x = 4 \\ x= -1 \rightarrow & y = -2x+2 = -2(-1)+2 = 4 \\ x= 4 \rightarrow & y = -2x+2 = -2(4)+2 = -6 \end{align}$
sehingga titik potongnya : (4,-6) dan (-1,4)
Jadi, titik potong yang lain adalah (-1,4). $ \heartsuit $
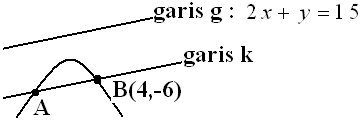
$\spadesuit \, $ Gradien garis g
$2x+y=15 \rightarrow m_g = \frac{-a}{b} = \frac{-2}{1} = -2 $
Garis k sejajar dengan garis g, sehingga gradiennya sama : $ m_k = m_g = -2 $
$\spadesuit \, $ Persamaan garis k
$y-y_1 = m(x-x_1) \rightarrow y-(-6) = -2(x-4) \rightarrow y = -2x + 2 $
$\spadesuit \, $ Menentukan titik potong garis k dan parabola
$\begin{align} y_1 & = y_2 \\ -2x+2 & = 6+x-x^2 \\ x^2-3x-4 & = 0 \\ (x+1)(x-4) & = 0 \\ x=-1 & \vee x = 4 \\ x= -1 \rightarrow & y = -2x+2 = -2(-1)+2 = 4 \\ x= 4 \rightarrow & y = -2x+2 = -2(4)+2 = -6 \end{align}$
sehingga titik potongnya : (4,-6) dan (-1,4)
Jadi, titik potong yang lain adalah (-1,4). $ \heartsuit $
Nomor 5
Persamaan kuadrat $ \, 3x^2-(a-1)x-1=0 \, $ mempunyai akar - akar $ x_1 \, $ dan $ \, x_2 \, $ , sedangkan persamaan kuadrat
yang akar-akarnya $ \frac{1}{x_1} \, $ dan $ \frac{1}{x_2} \, $ adalah $ \, x^2-(2b+1)x+b=0 \, $ .
Nilai $ \, 2a + b = .... $
$\clubsuit \, $ PK I : $ 3x^2 - (a-1)x - 1 = 0 \, $ akar-akarnya $ x_1 \, $ dan $ \, x_2$
$x_1+x_2 = \frac{-b}{a} = \frac{a-1}{3} \, $ dan $ \, x_1.x_2 = \frac{c}{a} = -\frac{1}{3} $
PK II : $ x^2-(2a+1)x+b = 0 \, $ akar-akarnya $ y_1 = \frac{1}{x_1} \, $ dan $ \, y_2 = \frac{1}{x_2} \, $ Operasi akar-akar PK II
$\begin{align} \text{operasi} & \text{ perkalian} : \, \, \\ y_1.y_2 & = \frac{c}{a} \\ \frac{1}{x_1} . \frac{1}{x_2} & = \frac{b}{1} \\ \frac{1}{x_1.x_2} & = b \\ \frac{1}{-\frac{1}{3}} & = b \\ -3 & = b \end{align}$ $\begin{align} \text{operasi} & \text{ penjumlahan} : \\ y_1+y_2 & = \frac{-b}{a} \\ \frac{1}{x_1} + \frac{1}{x_2} & = \frac{b}{1} \\ \frac{x_1+x_2}{x_1.x_2} & = \frac{2b+1}{1} \\ \frac{\frac{a-1}{3}}{-\frac{1}{3}} & = 2b+1 \\ 1-a & = 2b + 1 \\ 1-a & = 2.(-3) + 1 \rightarrow a = 6 \end{align}$
sehingga : $ 2a + b = 2.6 + (-3) = 9 $
Jadi, nilai $ 2a + b = 9. \heartsuit$
$x_1+x_2 = \frac{-b}{a} = \frac{a-1}{3} \, $ dan $ \, x_1.x_2 = \frac{c}{a} = -\frac{1}{3} $
PK II : $ x^2-(2a+1)x+b = 0 \, $ akar-akarnya $ y_1 = \frac{1}{x_1} \, $ dan $ \, y_2 = \frac{1}{x_2} \, $ Operasi akar-akar PK II
$\begin{align} \text{operasi} & \text{ perkalian} : \, \, \\ y_1.y_2 & = \frac{c}{a} \\ \frac{1}{x_1} . \frac{1}{x_2} & = \frac{b}{1} \\ \frac{1}{x_1.x_2} & = b \\ \frac{1}{-\frac{1}{3}} & = b \\ -3 & = b \end{align}$ $\begin{align} \text{operasi} & \text{ penjumlahan} : \\ y_1+y_2 & = \frac{-b}{a} \\ \frac{1}{x_1} + \frac{1}{x_2} & = \frac{b}{1} \\ \frac{x_1+x_2}{x_1.x_2} & = \frac{2b+1}{1} \\ \frac{\frac{a-1}{3}}{-\frac{1}{3}} & = 2b+1 \\ 1-a & = 2b + 1 \\ 1-a & = 2.(-3) + 1 \rightarrow a = 6 \end{align}$
sehingga : $ 2a + b = 2.6 + (-3) = 9 $
Jadi, nilai $ 2a + b = 9. \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.