Nomor 1
Diberikan limas $T.ABC$. Misalkan $u=\vec{TA}, v=\vec{TB}, w=\vec{TC}$. Jika $P$ titik berat $\Delta ABC$, maka $\vec{TP}=...$


$\clubsuit \, $ Titik P adalah titik berat, sehingga:
$\vec{AP}=\frac{2}{3}\vec{AD} \, $ dan $\vec{BD} : \vec{DC} = 1 : 1$
$\clubsuit \, $ Menentukan vektor $\vec{TD}$ dari gambar berikut:

$\vec{TD}=\frac{1.\vec{v}+1.\vec{w}}{1+1} = \frac{\vec{v}+\vec{w}}{2} $
$\clubsuit \, $ Menentukan vektor $\vec{AD}$ dan $\vec{AP}$ :
$\begin{align} \vec{AD}&=\vec{AT}+\vec{TD} \\ &=-\vec{u}+ \left( \frac{\vec{v}+\vec{w}}{2} \right) \\ \vec{AD}&= \frac{\vec{v}+\vec{w}-2\vec{u}}{2} \\ \vec{AP}&=\frac{2}{3}\vec{AD} \\ \vec{AP}&=\frac{2}{3}.\left( \frac{\vec{v}+\vec{w}-2\vec{u}}{2} \right) \\ \vec{AP}&=\frac{1}{3}(\vec{v}+\vec{w}-2\vec{u}) \end{align}$
$\clubsuit \, $ Menentukan vektor $\vec{TP}$ :
$\begin{align} \vec{TP}&=\vec{TA}+\vec{AP} \\ &=\vec{u}+ \frac{1}{3}(\vec{v}+\vec{w}-2\vec{u}) \\ &=\frac{1}{3}(\vec{u}+\vec{v}+\vec{w}) \end{align}$
Jadi, $\vec{TP}=\frac{1}{3}(\vec{u}+\vec{v}+\vec{w}). \heartsuit $
$\vec{AP}=\frac{2}{3}\vec{AD} \, $ dan $\vec{BD} : \vec{DC} = 1 : 1$
$\clubsuit \, $ Menentukan vektor $\vec{TD}$ dari gambar berikut:

$\vec{TD}=\frac{1.\vec{v}+1.\vec{w}}{1+1} = \frac{\vec{v}+\vec{w}}{2} $
$\clubsuit \, $ Menentukan vektor $\vec{AD}$ dan $\vec{AP}$ :
$\begin{align} \vec{AD}&=\vec{AT}+\vec{TD} \\ &=-\vec{u}+ \left( \frac{\vec{v}+\vec{w}}{2} \right) \\ \vec{AD}&= \frac{\vec{v}+\vec{w}-2\vec{u}}{2} \\ \vec{AP}&=\frac{2}{3}\vec{AD} \\ \vec{AP}&=\frac{2}{3}.\left( \frac{\vec{v}+\vec{w}-2\vec{u}}{2} \right) \\ \vec{AP}&=\frac{1}{3}(\vec{v}+\vec{w}-2\vec{u}) \end{align}$
$\clubsuit \, $ Menentukan vektor $\vec{TP}$ :
$\begin{align} \vec{TP}&=\vec{TA}+\vec{AP} \\ &=\vec{u}+ \frac{1}{3}(\vec{v}+\vec{w}-2\vec{u}) \\ &=\frac{1}{3}(\vec{u}+\vec{v}+\vec{w}) \end{align}$
Jadi, $\vec{TP}=\frac{1}{3}(\vec{u}+\vec{v}+\vec{w}). \heartsuit $
Nomor 2
Banyaknya akar real $f(t)=t^9-t$ adalah ... buah.
$\spadesuit \, $ Bentuk pemfaktoran :
$p^2-q^2=(p-q)(p+q)\, $ atau $\, p^n-1=(p^{n/2}-1)(p^{n/2}+1)$
dengan $n$ genap
$\spadesuit \, $ Untuk menentukan akar-akarnya, maka $f(t)=0$
$\begin{align} f(t)&=0 \\ t^9-t&=0 \\ t(t^8-1)&=0 \\ t(t^4-1)(t^4+1)&=0 \\ t(t^2-1)(t^2+1)(t^4+1)&=0 \\ t(t-1)(t+1)(t^2+1)(t^4+1)&=0 \end{align}$
$\spadesuit \, $ Sehingga akar-akarnya:
$t=0,t=1,t=-1$ dan $t^2=-1$ (tidak real) serta $t^4=-1$ (tidak real).
Jadi, akar-akar realnya ada tiga yaitu 0, 1, dan -1. $ \, \heartsuit $
$p^2-q^2=(p-q)(p+q)\, $ atau $\, p^n-1=(p^{n/2}-1)(p^{n/2}+1)$
dengan $n$ genap
$\spadesuit \, $ Untuk menentukan akar-akarnya, maka $f(t)=0$
$\begin{align} f(t)&=0 \\ t^9-t&=0 \\ t(t^8-1)&=0 \\ t(t^4-1)(t^4+1)&=0 \\ t(t^2-1)(t^2+1)(t^4+1)&=0 \\ t(t-1)(t+1)(t^2+1)(t^4+1)&=0 \end{align}$
$\spadesuit \, $ Sehingga akar-akarnya:
$t=0,t=1,t=-1$ dan $t^2=-1$ (tidak real) serta $t^4=-1$ (tidak real).
Jadi, akar-akar realnya ada tiga yaitu 0, 1, dan -1. $ \, \heartsuit $
Nomor 3
Bila $ \tan x = -\frac{3}{4}, \, \frac{3\pi}{2} < x < 2\pi , \, $ maka $ \sin \left( \frac{\pi}{3} - x \right) = .... $
$\clubsuit \, $ Buat segitiga dari $ \tan x = - \frac{3}{4} = \frac{de}{sa} $
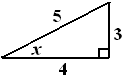
Sudut $ x \, $ ada di $ \frac{3\pi}{2} < x < 2\pi \, $ artinya kuadran 4, sehingga nilai sin negatif dan cos positif
nilai $ \sin x = - \frac{3}{5}, \, $ dan $ \cos x = \frac{4}{5} $
$\clubsuit \, $ Rumus dasar : $ \sin (A - B) = \sin A \cos B - \cos A \sin B $
$\clubsuit \, $ Maenentukan hasilnya
$\begin{align} \sin \left( \frac{\pi}{3} - x \right) & = \sin \left( 60^\circ - x \right) \\ & = \sin 60^\circ \cos x - \cos 60^\circ \sin x \\ & = \frac{1}{2} \sqrt{3} . \frac{4}{5} - \frac{1}{2} . (- \frac{3}{5} ) \\ & = \frac{4}{10} \sqrt{3} + \frac{3}{10} \\ & = \frac{4\sqrt{3} + 3}{10} \end{align}$
Jadi, nilai $ \sin \left( \frac{\pi}{3} - x \right) = \frac{4\sqrt{3} + 3}{10} . \heartsuit $

Sudut $ x \, $ ada di $ \frac{3\pi}{2} < x < 2\pi \, $ artinya kuadran 4, sehingga nilai sin negatif dan cos positif
nilai $ \sin x = - \frac{3}{5}, \, $ dan $ \cos x = \frac{4}{5} $
$\clubsuit \, $ Rumus dasar : $ \sin (A - B) = \sin A \cos B - \cos A \sin B $
$\clubsuit \, $ Maenentukan hasilnya
$\begin{align} \sin \left( \frac{\pi}{3} - x \right) & = \sin \left( 60^\circ - x \right) \\ & = \sin 60^\circ \cos x - \cos 60^\circ \sin x \\ & = \frac{1}{2} \sqrt{3} . \frac{4}{5} - \frac{1}{2} . (- \frac{3}{5} ) \\ & = \frac{4}{10} \sqrt{3} + \frac{3}{10} \\ & = \frac{4\sqrt{3} + 3}{10} \end{align}$
Jadi, nilai $ \sin \left( \frac{\pi}{3} - x \right) = \frac{4\sqrt{3} + 3}{10} . \heartsuit $
Nomor 4
Jika $ \alpha \, $ dan $ \beta \, $ adalah akar - akar persamaan kuadrat $ (m-1)x^2 - (m+2)x - 1 = 0, \, $
maka $ \log (1 + (1-\alpha ) \beta + \alpha ) \, $ ada nilainya untuk ....
$\spadesuit \, $ Konsep dasar logaritma
$ {}^a \log f(x) \, $ ada nilainya jika $ a > 0, \, a \neq 1, \, $ dan $ f(x) > 0 $
Sehingga syarat pada soal ini :
$ \log (1 + (1-\alpha ) \beta + \alpha ) \, $ ada nilai, syaratnya : $ (1 + (1-\alpha ) \beta + \alpha ) > 0 $
$\spadesuit \, $ PK $ (m-1)x^2 - (m+2)x - 1 = 0, \, $ akar-akarnya $ \alpha \, $ dan $ \beta $
$ \alpha + \beta = \frac{-b}{a} \rightarrow \alpha + \beta = \frac{m+2}{m-1} $
$ \alpha . \beta = \frac{c}{a} \rightarrow \alpha . \beta = \frac{-1}{m-1} $
$\spadesuit \, $ Menyelesaikan syaratnya
$\begin{align} (1 + (1-\alpha ) \beta + \alpha ) & > 0 \\ 1 + \beta - \alpha \beta + \alpha & > 0 \\ 1 + (\alpha + \beta ) - \alpha \beta & > 0 \\ 1 + \frac{m+2}{m-1} - \frac{-1}{m-1} & > 0 \\ \frac{m-1}{m-1} + \frac{m+2}{m-1} + \frac{1}{m-1} & > 0 \\ \frac{(m-1) + (m+2) + 1}{m-1} & > 0 \\ \frac{2m+2}{m-1} & > 0 \\ m = -1 \vee m & = 1 \end{align}$

Jadi, solusinya HP = $ \{ m < -1 \vee m > 1 \} . \heartsuit $
$ {}^a \log f(x) \, $ ada nilainya jika $ a > 0, \, a \neq 1, \, $ dan $ f(x) > 0 $
Sehingga syarat pada soal ini :
$ \log (1 + (1-\alpha ) \beta + \alpha ) \, $ ada nilai, syaratnya : $ (1 + (1-\alpha ) \beta + \alpha ) > 0 $
$\spadesuit \, $ PK $ (m-1)x^2 - (m+2)x - 1 = 0, \, $ akar-akarnya $ \alpha \, $ dan $ \beta $
$ \alpha + \beta = \frac{-b}{a} \rightarrow \alpha + \beta = \frac{m+2}{m-1} $
$ \alpha . \beta = \frac{c}{a} \rightarrow \alpha . \beta = \frac{-1}{m-1} $
$\spadesuit \, $ Menyelesaikan syaratnya
$\begin{align} (1 + (1-\alpha ) \beta + \alpha ) & > 0 \\ 1 + \beta - \alpha \beta + \alpha & > 0 \\ 1 + (\alpha + \beta ) - \alpha \beta & > 0 \\ 1 + \frac{m+2}{m-1} - \frac{-1}{m-1} & > 0 \\ \frac{m-1}{m-1} + \frac{m+2}{m-1} + \frac{1}{m-1} & > 0 \\ \frac{(m-1) + (m+2) + 1}{m-1} & > 0 \\ \frac{2m+2}{m-1} & > 0 \\ m = -1 \vee m & = 1 \end{align}$

Jadi, solusinya HP = $ \{ m < -1 \vee m > 1 \} . \heartsuit $
Nomor 5
Di antara 20.000 dan 70.000, banyak bilangan genap dengan tidak ada digit berulang adalah .....
$\clubsuit \, $ Konsep Dasar
*). Suatu bilangan genap syaratnya angka satuannya harus genap
*). tidak ada digit berulang artinya angka yang sudah dipakai tidak boleh dipakai lagi atau tidak ada digit yang sama.
$\clubsuit \, $ Menentukan banyak bilangannya
(i). Pilihan angka yang digunakan : 0,1,2,3,4,5,6,7,8 dan 9. Artinya ada 10 pilihan angka.
(ii). Agar bilangannya di antara 20.000 dan 70.000 maka puluh ribuannya harus 2,3,4,5, dan 6
(iii). Agar genap, maka satuannya harus genap yaitu 0,2,4,6, dan 8
Untuk mempermudah perhitungan, angka puluh ribuannya dibagi menjadi dua kasus yaitu yang genap dan yang ganjil :
Kasus I : puluh ribuannya genap
*). puluh ribuannya genap, ada 3 pilihan yaitu 2, 4, 6
*). satuannya ada 4 pilihan karena angka genap salah satunya sudah dipakai pada puluh ribuannya
*). ribuannya ada 8 pilihan karena dua angka sudah dipakai pada puluh ribuan dan satuan
*). ratusannya ada 7 pilihan karena tiga angka sudah dipakai untuk puluh ribuan, satuan dan ribuannya
*). puluhannya ada 6 pilihan sisa
cara I = 3.8.7.6.4 = 4032
Kasus II : puluh ribuannya ganjil
*). puluh ribuannya ganjil, ada 2 pilihan yaitu 3 atau 5
*). satuannya ada 5 pilihan yaitu 0,2,4,6,8
*). ribuannya ada 8 pilihan karena dua angka sudah dipakai pada puluh ribuan dan satuan
*). ratusannya ada 7 pilihan karena tiga angka sudah dipakai untuk puluh ribuan, satuan dan ribuannya
*). puluhannya ada 6 pilihan sisa
cara II = 2.8.7.6.5 = 3360
Sehingga total cara = cara I + cara II = 4032 + 3360 = 7392
Jadi, banyak bilangan yang terbentuk ada 7.392 bilangan. $ \heartsuit$
*). Suatu bilangan genap syaratnya angka satuannya harus genap
*). tidak ada digit berulang artinya angka yang sudah dipakai tidak boleh dipakai lagi atau tidak ada digit yang sama.
$\clubsuit \, $ Menentukan banyak bilangannya
(i). Pilihan angka yang digunakan : 0,1,2,3,4,5,6,7,8 dan 9. Artinya ada 10 pilihan angka.
(ii). Agar bilangannya di antara 20.000 dan 70.000 maka puluh ribuannya harus 2,3,4,5, dan 6
(iii). Agar genap, maka satuannya harus genap yaitu 0,2,4,6, dan 8
Untuk mempermudah perhitungan, angka puluh ribuannya dibagi menjadi dua kasus yaitu yang genap dan yang ganjil :
Kasus I : puluh ribuannya genap
*). puluh ribuannya genap, ada 3 pilihan yaitu 2, 4, 6
*). satuannya ada 4 pilihan karena angka genap salah satunya sudah dipakai pada puluh ribuannya
*). ribuannya ada 8 pilihan karena dua angka sudah dipakai pada puluh ribuan dan satuan
*). ratusannya ada 7 pilihan karena tiga angka sudah dipakai untuk puluh ribuan, satuan dan ribuannya
*). puluhannya ada 6 pilihan sisa
cara I = 3.8.7.6.4 = 4032
Kasus II : puluh ribuannya ganjil
*). puluh ribuannya ganjil, ada 2 pilihan yaitu 3 atau 5
*). satuannya ada 5 pilihan yaitu 0,2,4,6,8
*). ribuannya ada 8 pilihan karena dua angka sudah dipakai pada puluh ribuan dan satuan
*). ratusannya ada 7 pilihan karena tiga angka sudah dipakai untuk puluh ribuan, satuan dan ribuannya
*). puluhannya ada 6 pilihan sisa
cara II = 2.8.7.6.5 = 3360
Sehingga total cara = cara I + cara II = 4032 + 3360 = 7392
Jadi, banyak bilangan yang terbentuk ada 7.392 bilangan. $ \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.