Nomor 6
Grafik fungsi kuadrat $ y = ax^2 + bx + c \, $ melalui titik (5,0) , (10,0) , dan (0,10). Jika titik minimum fungsi
dicapai di titik $( x_0 , y_0) \, $ , maka $ x_0 + y_0 \, $ adalah ....
$\spadesuit \, $ Konsep Dasar
*) Menyusun FK melalui tipot sumbu X di ($x_1,0$) dan ($x_2,0$)
FK : $ y = a(x-x_1)(x-x_2) $
*) Titik puncaknya ($x_p,y_p$) :
$ x_p = \frac{-b}{2a} \, $ dan $ y_p = \frac{D}{-4a} \, $ dengan $ D = b^2 - 4ac $
$\spadesuit \, $ Menyusun FK melalu titik (5,0) dan (10,0) artinya $ x_1 = 5 \, $ dan $ x_2 = 10 $
FK : $ y = a(x-x_1)(x-x_2) \rightarrow y = a(x-5)(x-10) $
$\spadesuit \, $ Substitusi titik (0,10) ke FK
$\begin{align} (x,y) = (0,10) \rightarrow y & = a(x-5)(x-10) \\ 10 & = a(0-5)(0-10) \\ 10 & = a(-5)(-10) \\ 10 & = 50a \\ a & = \frac{10}{50} = \frac{1}{5} \end{align}$
FK menjadi :
$ y = a(x-5)(x-10) = \frac{1}{5}(x-5)(x-10) $
$ y = \frac{1}{5}x^2 - 3x + 10 $
$\spadesuit \, $ Menentukan titik puncak $(x_p,y_p) = (x_0,y_0) $
FK : $ y = \frac{1}{5}x^2 - 3x + 10 \rightarrow a = \frac{1}{5}, \, b = -3, \, c = 10 $
$\begin{align} *) \, x_0 = x_p & = \frac{-b}{2a} = \frac{-(-3)}{2.\frac{1}{5}} = \frac{15}{2} \\ *) \, y_0 = y_p & = \frac{D}{-4a} = \frac{b^2-4ac}{-4a} \\ & = \frac{(-3)^2 - 4. \frac{1}{5}. 10 }{-4.\frac{4}{5}} \\ & = \frac{9-8}{-\frac{4}{5}} = - \frac{5}{4} \end{align}$
Sehingga nilai : $ x_0 + y_0 = \frac{15}{2} + (-\frac{5}{4}) = \frac{25}{4} $
Jadi, nilai $ x_0 + y_0 = \frac{25}{4} . \heartsuit $
*) Menyusun FK melalui tipot sumbu X di ($x_1,0$) dan ($x_2,0$)
FK : $ y = a(x-x_1)(x-x_2) $
*) Titik puncaknya ($x_p,y_p$) :
$ x_p = \frac{-b}{2a} \, $ dan $ y_p = \frac{D}{-4a} \, $ dengan $ D = b^2 - 4ac $
$\spadesuit \, $ Menyusun FK melalu titik (5,0) dan (10,0) artinya $ x_1 = 5 \, $ dan $ x_2 = 10 $
FK : $ y = a(x-x_1)(x-x_2) \rightarrow y = a(x-5)(x-10) $
$\spadesuit \, $ Substitusi titik (0,10) ke FK
$\begin{align} (x,y) = (0,10) \rightarrow y & = a(x-5)(x-10) \\ 10 & = a(0-5)(0-10) \\ 10 & = a(-5)(-10) \\ 10 & = 50a \\ a & = \frac{10}{50} = \frac{1}{5} \end{align}$
FK menjadi :
$ y = a(x-5)(x-10) = \frac{1}{5}(x-5)(x-10) $
$ y = \frac{1}{5}x^2 - 3x + 10 $
$\spadesuit \, $ Menentukan titik puncak $(x_p,y_p) = (x_0,y_0) $
FK : $ y = \frac{1}{5}x^2 - 3x + 10 \rightarrow a = \frac{1}{5}, \, b = -3, \, c = 10 $
$\begin{align} *) \, x_0 = x_p & = \frac{-b}{2a} = \frac{-(-3)}{2.\frac{1}{5}} = \frac{15}{2} \\ *) \, y_0 = y_p & = \frac{D}{-4a} = \frac{b^2-4ac}{-4a} \\ & = \frac{(-3)^2 - 4. \frac{1}{5}. 10 }{-4.\frac{4}{5}} \\ & = \frac{9-8}{-\frac{4}{5}} = - \frac{5}{4} \end{align}$
Sehingga nilai : $ x_0 + y_0 = \frac{15}{2} + (-\frac{5}{4}) = \frac{25}{4} $
Jadi, nilai $ x_0 + y_0 = \frac{25}{4} . \heartsuit $
Nomor 7
Pada segitiga siku-siku ABC dengan $ AC \bot BC \, $ dan panjang $ AC \, $ adalah $ \frac{5}{2} BC \, $ .
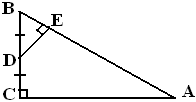
Jika D titik tengah BC dan $ DE \bot AB \, $ , maka perbandingan luas daerah $ \Delta ABC : \Delta DBE \, $ adalah ....

Jika D titik tengah BC dan $ DE \bot AB \, $ , maka perbandingan luas daerah $ \Delta ABC : \Delta DBE \, $ adalah ....
$\clubsuit \,$ Gambar

Misal panjang $ BD = x , \, $ panjang yang lainnya :
$ CD = x, \, BC = 2x $
$ AC = \frac{5}{2}BC = \frac{5}{2}.2x = 5x $
$ AB = \sqrt{AC^2 + BC^2 } = \sqrt{(5x)^2 + (2x)^2} $
$ AB = \sqrt{29x^2}=x\sqrt{29} $
$\clubsuit \,$ Menentukan panjang BE dan ED dengan konsep kesebangunan
$ \Delta BED \, $ sebangun dengan $ \Delta ABC \, $ pada gambar 2 dan gambar 3
$ \frac{BE}{BC}=\frac{BD}{BA} \rightarrow \frac{BE}{2x}=\frac{x}{x\sqrt{29}} \rightarrow BE = \frac{2x}{\sqrt{29}} $
$ \frac{ED}{AC}=\frac{BD}{BA} \rightarrow \frac{ED}{5x}=\frac{x}{x\sqrt{29}} \rightarrow ED = \frac{5x}{\sqrt{29}} $
$\clubsuit \,$ Menentukan perbandingan luasnya
$\begin{align} \frac{L \, \Delta ABC }{L \, \Delta DBE } & = \frac{\frac{1}{2}. AC.BC}{\frac{1}{2}.ED.BE} \\ & = \frac{\frac{1}{2}. 5x.2x}{\frac{1}{2}.\frac{5x}{\sqrt{29}}.\frac{2x}{\sqrt{29}}} \\ & = 5x.2x. \frac{\sqrt{29}}{5x} . \frac{\sqrt{29}}{2x} \\ & = \frac{29}{1} \end{align}$
Jadi, perbandingan luasnya adalah 29 : 1 . $\heartsuit $

Misal panjang $ BD = x , \, $ panjang yang lainnya :
$ CD = x, \, BC = 2x $
$ AC = \frac{5}{2}BC = \frac{5}{2}.2x = 5x $
$ AB = \sqrt{AC^2 + BC^2 } = \sqrt{(5x)^2 + (2x)^2} $
$ AB = \sqrt{29x^2}=x\sqrt{29} $
$\clubsuit \,$ Menentukan panjang BE dan ED dengan konsep kesebangunan
$ \Delta BED \, $ sebangun dengan $ \Delta ABC \, $ pada gambar 2 dan gambar 3
$ \frac{BE}{BC}=\frac{BD}{BA} \rightarrow \frac{BE}{2x}=\frac{x}{x\sqrt{29}} \rightarrow BE = \frac{2x}{\sqrt{29}} $
$ \frac{ED}{AC}=\frac{BD}{BA} \rightarrow \frac{ED}{5x}=\frac{x}{x\sqrt{29}} \rightarrow ED = \frac{5x}{\sqrt{29}} $
$\clubsuit \,$ Menentukan perbandingan luasnya
$\begin{align} \frac{L \, \Delta ABC }{L \, \Delta DBE } & = \frac{\frac{1}{2}. AC.BC}{\frac{1}{2}.ED.BE} \\ & = \frac{\frac{1}{2}. 5x.2x}{\frac{1}{2}.\frac{5x}{\sqrt{29}}.\frac{2x}{\sqrt{29}}} \\ & = 5x.2x. \frac{\sqrt{29}}{5x} . \frac{\sqrt{29}}{2x} \\ & = \frac{29}{1} \end{align}$
Jadi, perbandingan luasnya adalah 29 : 1 . $\heartsuit $
Nomor 8
Jika pertidaksamaan $ 3x -p > \frac{x-2}{3} + px \, $ mempunyai penyelesaian $ x > 5 , \, $ maka nilai $ p \, $ adalah ....
$\spadesuit \, $ Kelompokkan pertidaksamaan
$\begin{align} 3x -p & > \frac{x-2}{3} + px \, \, \, \, \text{(kali 3)} \\ 9x - 3p & > x-2 + 3px \\ 9x - x - 3px & > 3p - 2 \\ (8-3p)x & > 3p - 2 \\ x & > \frac{3p-2}{8-3p} \, \, \, \, \text{...pert(i)} \end{align}$
Solusi pertidaksamaan $ x > 5 \, $ , artinya bentuk $ x > \frac{3p-2}{8-3p} \, $ sama dengan $ x > 5 \, $ , sehingga diperoleh $ \frac{3p-2}{8-3p} = 5 $
$\spadesuit \, $ Menentukan nilai $ p $
$\begin{align} \frac{3p-2}{8-3p} & = 5 \\ 3p-2 & = 5(8-3p) \\ 3p-2 & = 40 - 15p \\ 18p & = 42 \\ p & = \frac{42}{18} = \frac{7}{3} \end{align}$
Jadi, nilai $ p = \frac{7}{3} . \heartsuit $
Catatan : tidak ada pada pilihan.
$\begin{align} 3x -p & > \frac{x-2}{3} + px \, \, \, \, \text{(kali 3)} \\ 9x - 3p & > x-2 + 3px \\ 9x - x - 3px & > 3p - 2 \\ (8-3p)x & > 3p - 2 \\ x & > \frac{3p-2}{8-3p} \, \, \, \, \text{...pert(i)} \end{align}$
Solusi pertidaksamaan $ x > 5 \, $ , artinya bentuk $ x > \frac{3p-2}{8-3p} \, $ sama dengan $ x > 5 \, $ , sehingga diperoleh $ \frac{3p-2}{8-3p} = 5 $
$\spadesuit \, $ Menentukan nilai $ p $
$\begin{align} \frac{3p-2}{8-3p} & = 5 \\ 3p-2 & = 5(8-3p) \\ 3p-2 & = 40 - 15p \\ 18p & = 42 \\ p & = \frac{42}{18} = \frac{7}{3} \end{align}$
Jadi, nilai $ p = \frac{7}{3} . \heartsuit $
Catatan : tidak ada pada pilihan.
Cara II :
$\spadesuit \, $ Solusi pertidaksamaan $ x > 5 , \, $ artinya $ x = 5\, $ adalah akar dari pertidaksamaannya. Substitusi $ x= 5 \, $ ke pertidaksamaanya dan tanda ketaksamaanya $ ( > , \, \geq , \, \leq , \, < ) \, $ menjadi sama dengan.
$\begin{align} x=5 \rightarrow 3x -p & > \frac{x-2}{3} + px \\ 3.5 -p & = \frac{5-2}{3} + p.5 \\ 15 -p & = \frac{3}{3} + 5p \\ 15 -p & = 1 + 5p \\ 6p & = 14 \\ p & = \frac{14}{6} = \frac{7}{3} \end{align}$
Jadi, nilai $ p = \frac{7}{3} . \heartsuit $
Catatan : tidak ada pada pilihan.
$\spadesuit \, $ Solusi pertidaksamaan $ x > 5 , \, $ artinya $ x = 5\, $ adalah akar dari pertidaksamaannya. Substitusi $ x= 5 \, $ ke pertidaksamaanya dan tanda ketaksamaanya $ ( > , \, \geq , \, \leq , \, < ) \, $ menjadi sama dengan.
$\begin{align} x=5 \rightarrow 3x -p & > \frac{x-2}{3} + px \\ 3.5 -p & = \frac{5-2}{3} + p.5 \\ 15 -p & = \frac{3}{3} + 5p \\ 15 -p & = 1 + 5p \\ 6p & = 14 \\ p & = \frac{14}{6} = \frac{7}{3} \end{align}$
Jadi, nilai $ p = \frac{7}{3} . \heartsuit $
Catatan : tidak ada pada pilihan.
Nomor 9
Perhatikan gambar $ \Delta PQR \, $ dengan $ \angle Q = 30^\circ , \, $ RS adalah garis tinggi dari titik sudut R. Jika $ QR = a \, $
dan $ PR = \frac{1}{2}\sqrt{3}a , \, $ maka rasio $ PR \, $ terhadap $ SQ \, $ adalah ....
$\clubsuit \,$ gambar

$\clubsuit \,$ Menentukan panjang SQ pada segitiga QRS
$\begin{align} \cos 30^\circ & = \frac{SQ}{QR} \\ \frac{1}{2}\sqrt{3} & = \frac{SQ}{a} \\ SQ & = \frac{1}{2}\sqrt{3}a \end{align}$
$\clubsuit \,$ Menentukan rasio (perbandingan)
$\begin{align} \frac{PR}{SQ} & = \frac{\frac{1}{2}\sqrt{3}a}{\frac{1}{2}\sqrt{3}a} = 1 \end{align}$
Jadi, rasio PR terhadap SQ adalah 1. $ \heartsuit $

$\clubsuit \,$ Menentukan panjang SQ pada segitiga QRS
$\begin{align} \cos 30^\circ & = \frac{SQ}{QR} \\ \frac{1}{2}\sqrt{3} & = \frac{SQ}{a} \\ SQ & = \frac{1}{2}\sqrt{3}a \end{align}$
$\clubsuit \,$ Menentukan rasio (perbandingan)
$\begin{align} \frac{PR}{SQ} & = \frac{\frac{1}{2}\sqrt{3}a}{\frac{1}{2}\sqrt{3}a} = 1 \end{align}$
Jadi, rasio PR terhadap SQ adalah 1. $ \heartsuit $
Nomor 10
Sebuah cakram yang terbuat dari logam mengalami pemuaian sehingga jari-jarinya bertambah 20% dari jari-jari semula.
Berapa persen pertambahan luas cakram tersebut dengan adanya pemuaian ?
$\spadesuit \, $ Permisalan
$ L_a \, $ = luas awal cakram = $ \pi r^2 $
$ r \, $ = jari-jari awal cakram
$ L_p \, $ = Luas adanya pemuaian = $ \pi (r_p)^2 $
$ r_p \, $ = jari-jari adanya pemuaian
$\spadesuit \, $ Jari-jari bertambah 20%
$\begin{align} r_p & = r + 20\% r = r + 0,2r = 1,2r \end{align}$
$\spadesuit \, $ Luas adanya pemuaian
$\begin{align} L_p & = \pi (r_p)^2 \\ & = \pi (1,2r)^2 \\ & = 1,44\pi r^2 \\ & = \pi r^2 + 0,44 \pi r^2 \\ & = \pi r^2 + 0,44 \times 100\% \pi r^2 \\ & = \pi r^2 + 44 \% \pi r^2 \end{align}$
Artinya Luas adanya pemuaian bertambah 44% dari luas awalnya sebelum adanya pemuaian.
Jadi, luasnya bertambah 44% . $ \heartsuit $
$ L_a \, $ = luas awal cakram = $ \pi r^2 $
$ r \, $ = jari-jari awal cakram
$ L_p \, $ = Luas adanya pemuaian = $ \pi (r_p)^2 $
$ r_p \, $ = jari-jari adanya pemuaian
$\spadesuit \, $ Jari-jari bertambah 20%
$\begin{align} r_p & = r + 20\% r = r + 0,2r = 1,2r \end{align}$
$\spadesuit \, $ Luas adanya pemuaian
$\begin{align} L_p & = \pi (r_p)^2 \\ & = \pi (1,2r)^2 \\ & = 1,44\pi r^2 \\ & = \pi r^2 + 0,44 \pi r^2 \\ & = \pi r^2 + 0,44 \times 100\% \pi r^2 \\ & = \pi r^2 + 44 \% \pi r^2 \end{align}$
Artinya Luas adanya pemuaian bertambah 44% dari luas awalnya sebelum adanya pemuaian.
Jadi, luasnya bertambah 44% . $ \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.