Nomor 21
Seutas tali dipotong menjasi 6 bagian sehingga potongan-potongan tersebut membentuk deret geometri. Jika tali terpendek 5 cm dan tali terplanjang
160 cm, panjang tali tersebut sebelum dipotong adalah ...
$\spadesuit \, $ Barisan geometri : $u_n=ar^{n-1}$ dan $s_n = \frac{a(r^n-1)}{r-1}$
Diketahui $a=5, u_6=160 , n=6$
$u_6=160 \Leftrightarrow ar^5=160 \Leftrightarrow 5r^5=160 \Leftrightarrow r=2$
$\spadesuit \, $ Menentukan panjang total talinya ($s_6$) :
$\begin{align*} s_n &= \frac{a(r^n-1)}{r-1} \\ s_6 &= \frac{5(2^6-1)}{2-1} \\ &= 5. 36 =315 \end{align*}$
Jadi, panjang tali sebelumnya adalah 315 cm .$ \heartsuit$
Diketahui $a=5, u_6=160 , n=6$
$u_6=160 \Leftrightarrow ar^5=160 \Leftrightarrow 5r^5=160 \Leftrightarrow r=2$
$\spadesuit \, $ Menentukan panjang total talinya ($s_6$) :
$\begin{align*} s_n &= \frac{a(r^n-1)}{r-1} \\ s_6 &= \frac{5(2^6-1)}{2-1} \\ &= 5. 36 =315 \end{align*}$
Jadi, panjang tali sebelumnya adalah 315 cm .$ \heartsuit$
Nomor 22
Diketahui balok KLMN.PQRS dengan KL = 3 cm , LM = 4 cm, dan KP = 12 cm. Jarak titik R ke garis PM adalah ....
$\clubsuit \,$ Gambar balok dan segitiganya :

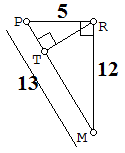
$\clubsuit \,$ Gunakan luas segitiga PMR :
$\begin{align*} L_{\Delta PMR} &= L_{\Delta PMR} \\ \frac{1}{2}.PM.TR &= \frac{1}{2}.RM.RP \, \, \text{(coret } \, \frac{1}{2} ) \\ PM.TR &= RM.RP \\ 13.TR &= 12.5 \\ TR &= \frac{60}{13} \end{align*}$
Jadi, panjang $TR = \frac{60}{13} $ cm. $ \heartsuit $


$\clubsuit \,$ Gunakan luas segitiga PMR :
$\begin{align*} L_{\Delta PMR} &= L_{\Delta PMR} \\ \frac{1}{2}.PM.TR &= \frac{1}{2}.RM.RP \, \, \text{(coret } \, \frac{1}{2} ) \\ PM.TR &= RM.RP \\ 13.TR &= 12.5 \\ TR &= \frac{60}{13} \end{align*}$
Jadi, panjang $TR = \frac{60}{13} $ cm. $ \heartsuit $
Nomor 23
Kubus ABCD.EFGH memiliki rusuk 4 cm. Sudut antara AE dan bidang AFH adalah $\alpha$ . Nilai $\sin \alpha = ...$
$\spadesuit \, $ Gambar balok dan segitiganya :


$\spadesuit \, $ Menentukan sinus sudutnya :
$\angle (EA, \Delta AFH ) = \angle ( AE,AP) = \theta $
$\begin{align*} \sin \theta &= \frac{EP}{AP} = \frac {2\sqrt{2}}{2\sqrt{6}} = \frac {\sqrt{2}}{\sqrt{6}} . \frac {\sqrt{6}}{\sqrt{6}} = \frac {\sqrt{12}}{6} = \frac {2\sqrt{3}}{6} \\ \sin \theta &= \frac {\sqrt{3}}{3} = \frac{1}{3}\sqrt{3} \end{align*}$
Jadi, nilai $\sin \theta = \frac{1}{3}\sqrt{3} . \heartsuit $


$\spadesuit \, $ Menentukan sinus sudutnya :
$\angle (EA, \Delta AFH ) = \angle ( AE,AP) = \theta $
$\begin{align*} \sin \theta &= \frac{EP}{AP} = \frac {2\sqrt{2}}{2\sqrt{6}} = \frac {\sqrt{2}}{\sqrt{6}} . \frac {\sqrt{6}}{\sqrt{6}} = \frac {\sqrt{12}}{6} = \frac {2\sqrt{3}}{6} \\ \sin \theta &= \frac {\sqrt{3}}{3} = \frac{1}{3}\sqrt{3} \end{align*}$
Jadi, nilai $\sin \theta = \frac{1}{3}\sqrt{3} . \heartsuit $
Nomor 24
Diketahui jajargenjang seperti gambar.
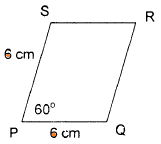
Panjang diagonal PR = ...

Panjang diagonal PR = ...
Cara I :
$\clubsuit \, $ Gambar lengkapnya :
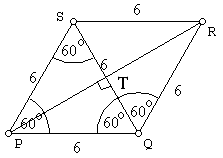
$\clubsuit \, $ Aturan cosinus pada sisi $PR$ :
$\begin{align*} PR^2 &= QP^2 + QR^2 - 2.QP.QR. \cos PQR \\ &= 6^2 + 6^2 - 2.6.6.\cos 120^o \\ &= 36+36 - 72. (-\frac{1}{2}) \\ &= 72+ 36 \\ PR^2 &= 108 \\ PR &= \sqrt{108}=6\sqrt{3} \end{align*}$
Jadi, panjang $PR =6\sqrt{3}. \heartsuit$
$\clubsuit \, $ Gambar lengkapnya :

$\clubsuit \, $ Aturan cosinus pada sisi $PR$ :
$\begin{align*} PR^2 &= QP^2 + QR^2 - 2.QP.QR. \cos PQR \\ &= 6^2 + 6^2 - 2.6.6.\cos 120^o \\ &= 36+36 - 72. (-\frac{1}{2}) \\ &= 72+ 36 \\ PR^2 &= 108 \\ PR &= \sqrt{108}=6\sqrt{3} \end{align*}$
Jadi, panjang $PR =6\sqrt{3}. \heartsuit$
Cara II :
$\clubsuit \, $ Gambar lengkapnya :

$\clubsuit \, $ Perhatikan segitiga $PQT$ :
$\begin{align*} \sin Q &= \frac{PT}{PQ} \\ \sin 60^o &= \frac{PT}{6} \\ \frac{1}{2} \sqrt{3} &= \frac{PT}{6} \\ PT &= 6. \frac{1}{2} \sqrt{3} \\ PT &= 3\sqrt{3} \end{align*}$
Jadi, panjang $PR =2.PT=2\times 3\sqrt{3}=6\sqrt{3}. \heartsuit$
$\clubsuit \, $ Gambar lengkapnya :

$\clubsuit \, $ Perhatikan segitiga $PQT$ :
$\begin{align*} \sin Q &= \frac{PT}{PQ} \\ \sin 60^o &= \frac{PT}{6} \\ \frac{1}{2} \sqrt{3} &= \frac{PT}{6} \\ PT &= 6. \frac{1}{2} \sqrt{3} \\ PT &= 3\sqrt{3} \end{align*}$
Jadi, panjang $PR =2.PT=2\times 3\sqrt{3}=6\sqrt{3}. \heartsuit$
Cara III :
$\clubsuit \, $ Gambar lengkapnya :

$\clubsuit \, $ Perhatikan segitiga $PQT$ , $QT=\frac{1}{2} QS=3$ dan gunakan pythagoras:
$\begin{align*} PT &= \sqrt{PQ^2-QT^2} \\ &= \sqrt{6^2-3^2} \\ &= \sqrt{36-9} \\ &= \sqrt{27} \\ PT &= 3\sqrt{3} \end{align*}$
Jadi, panjang $PR =2.PT=2\times 3\sqrt{3}=6\sqrt{3}. \heartsuit$
$\clubsuit \, $ Gambar lengkapnya :

$\clubsuit \, $ Perhatikan segitiga $PQT$ , $QT=\frac{1}{2} QS=3$ dan gunakan pythagoras:
$\begin{align*} PT &= \sqrt{PQ^2-QT^2} \\ &= \sqrt{6^2-3^2} \\ &= \sqrt{36-9} \\ &= \sqrt{27} \\ PT &= 3\sqrt{3} \end{align*}$
Jadi, panjang $PR =2.PT=2\times 3\sqrt{3}=6\sqrt{3}. \heartsuit$
Nomor 25
Himpunan penyelesaian dari persamaan $2\cos ^2x + 5\sin x-4 = 0$ untuk $0^o \leq x \leq 360^o $ adalah ...
$\spadesuit \, $ Misalkan $p=\sin x $ dan gunakan $\sin ^2x + \cos ^2x =1 $ :
$\begin{align*} 2\cos ^2x + 5\sin x-4 &= 0 \\ 2(1-\sin ^2x) + 5\sin x-4 &= 0 \\ 2-2\sin ^2x + 5\sin x-4 &= 0 \\ 2\sin ^2x -5\sin x +2 &= 0 \\ 2p^2-5p+2 &= 0 \\ (2p-1)(p-2) &= 0 \\ p=\frac{1}{2} \, &\text{atau} \, p=2 \\ p=\frac{1}{2} \Rightarrow & \sin x =\frac{1}{2} \Rightarrow x=\{30^o, 150^o\} \\ p=2 \Rightarrow & \sin x =2 \, \text{(tidak ada nilai} \, x \, \text{ yang memenuhi )} \\ &\text{(nilai maksimum dari} \, \sin x \, \text{adalah 1)} \end{align*}$
Jadi, $HP=\{ 30^o, 150^o\} .\heartsuit $
$\begin{align*} 2\cos ^2x + 5\sin x-4 &= 0 \\ 2(1-\sin ^2x) + 5\sin x-4 &= 0 \\ 2-2\sin ^2x + 5\sin x-4 &= 0 \\ 2\sin ^2x -5\sin x +2 &= 0 \\ 2p^2-5p+2 &= 0 \\ (2p-1)(p-2) &= 0 \\ p=\frac{1}{2} \, &\text{atau} \, p=2 \\ p=\frac{1}{2} \Rightarrow & \sin x =\frac{1}{2} \Rightarrow x=\{30^o, 150^o\} \\ p=2 \Rightarrow & \sin x =2 \, \text{(tidak ada nilai} \, x \, \text{ yang memenuhi )} \\ &\text{(nilai maksimum dari} \, \sin x \, \text{adalah 1)} \end{align*}$
Jadi, $HP=\{ 30^o, 150^o\} .\heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.