Nomor 36
Data berat badan (dalam kg) 30 balita seperti disajikan dalam histogram berikut.

Median dari data tersebut adalah ...

Median dari data tersebut adalah ...
$\spadesuit \, $ Total data : $n=2+7+12+6+3=30$
$\spadesuit \, $ Letak median = kuartil 2 ($Q_2$) :
$Q_i=X_{\frac{i.n+2}{4}} \Rightarrow Q_2=X_{\frac{2.30+2}{4}}=X_{15,5}$
artinya median terletak antara data ke 15 dan 16 yaitu pada interval : 8,5 - 11,5
tepi bawah : $tb=8,5$ dan panjang kelas : $c=11,5-8,5=3$
$\spadesuit \, $ Rumus dasar : $Q_i=tb + \frac{\frac{i}{4}.n-fks_{Q_2}}{f_{Q_2}}.c$
keterangan :
$f_{Q_2} = \,$ frekuensi kelas $Q_2$ = 12
$ fks_{Q_2} = \, $ frekuensi kumulatif sebelum kelas $Q_2$ = 2+7 = 9
$\spadesuit \, $ Menentukan median ($Q_2$)
$\begin{align*} Median = Q_2 &= tb + \frac{\frac{2}{4}.n-fks_{Q_2}}{f_{Q_2}}.c \\ &= 8,5 + \frac{\frac{1}{2}.30-9}{12}.3 \\ &= 8,5 + \frac{6}{4} \\ &= 8,5 + 1,5 \\ &= 10 \end{align*}$
Jadi, nilai mediannya adalah 10.$ \heartsuit$
$\spadesuit \, $ Letak median = kuartil 2 ($Q_2$) :
$Q_i=X_{\frac{i.n+2}{4}} \Rightarrow Q_2=X_{\frac{2.30+2}{4}}=X_{15,5}$
artinya median terletak antara data ke 15 dan 16 yaitu pada interval : 8,5 - 11,5
tepi bawah : $tb=8,5$ dan panjang kelas : $c=11,5-8,5=3$
$\spadesuit \, $ Rumus dasar : $Q_i=tb + \frac{\frac{i}{4}.n-fks_{Q_2}}{f_{Q_2}}.c$
keterangan :
$f_{Q_2} = \,$ frekuensi kelas $Q_2$ = 12
$ fks_{Q_2} = \, $ frekuensi kumulatif sebelum kelas $Q_2$ = 2+7 = 9
$\spadesuit \, $ Menentukan median ($Q_2$)
$\begin{align*} Median = Q_2 &= tb + \frac{\frac{2}{4}.n-fks_{Q_2}}{f_{Q_2}}.c \\ &= 8,5 + \frac{\frac{1}{2}.30-9}{12}.3 \\ &= 8,5 + \frac{6}{4} \\ &= 8,5 + 1,5 \\ &= 10 \end{align*}$
Jadi, nilai mediannya adalah 10.$ \heartsuit$
Nomor 37
Kuartil atas dari data pada tabel berikut adalah ...
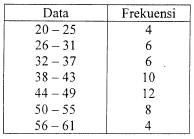

$\clubsuit \, $ Total data : $n=4+6+6+10+12+8+4=50$
$\clubsuit \, $ Letak kuartil atas = kuartil 3 ($Q_3$) :
$Q_i=X_{\frac{i.n+2}{4}} \Rightarrow Q_3=X_{\frac{3.50+2}{4}}=X_38$
artinya kuartil atas terletak pada data ke 38 yaitu pada interval : 44 - 49
tepi bawah : $tb=44-0,5=43,5$ dan panjang kelas : $c=49-44+1=6$
$\clubsuit \, $ Rumus dasar : $Q_i=tb + \frac{\frac{i}{4}.n-fks_{Q_3}}{f_{Q_3}}.c$
keterangan :
$f_{Q_3} = \,$ frekuensi kelas $Q_3$ = 12
$ fks_{Q_3} = \, $ frekuensi kumulatif sebelum kelas $Q_3$ = 4+6+6+10 = 26
$\clubsuit \, $ Menentukan kuartil atas ($Q_3$)
$\begin{align*} Kuartil \, atas = Q_3 &= tb + \frac{\frac{3}{4}.n-fks_{Q_3}}{f_{Q_3}}.c \\ &= 43,5 + \frac{\frac{3}{4}.50-26}{12}.6 \\ &= 43,5 + \frac{11,5}{2} \\ &= 43,5 + 5,75 \\ &= 49,25 \end{align*}$
Jadi, nilai kuartil atasnya adalah 49,25.$ \heartsuit$
$\clubsuit \, $ Letak kuartil atas = kuartil 3 ($Q_3$) :
$Q_i=X_{\frac{i.n+2}{4}} \Rightarrow Q_3=X_{\frac{3.50+2}{4}}=X_38$
artinya kuartil atas terletak pada data ke 38 yaitu pada interval : 44 - 49
tepi bawah : $tb=44-0,5=43,5$ dan panjang kelas : $c=49-44+1=6$
$\clubsuit \, $ Rumus dasar : $Q_i=tb + \frac{\frac{i}{4}.n-fks_{Q_3}}{f_{Q_3}}.c$
keterangan :
$f_{Q_3} = \,$ frekuensi kelas $Q_3$ = 12
$ fks_{Q_3} = \, $ frekuensi kumulatif sebelum kelas $Q_3$ = 4+6+6+10 = 26
$\clubsuit \, $ Menentukan kuartil atas ($Q_3$)
$\begin{align*} Kuartil \, atas = Q_3 &= tb + \frac{\frac{3}{4}.n-fks_{Q_3}}{f_{Q_3}}.c \\ &= 43,5 + \frac{\frac{3}{4}.50-26}{12}.6 \\ &= 43,5 + \frac{11,5}{2} \\ &= 43,5 + 5,75 \\ &= 49,25 \end{align*}$
Jadi, nilai kuartil atasnya adalah 49,25.$ \heartsuit$
Nomor 38
Joni mempunyai koleksi 3 pasang sepatu dengan merk yang berbeda, 4 baju berlainan coraknya, dan 3 celana yang berbeda warna.
Banyak cara berpakaian Joni dengan penampilan yang berbeda adalah ...
$\spadesuit \, $ Misalkan : S = sepatu, B = baju, C = celana
$\spadesuit \, $ Ada 3S, 4B, dan 3C
$\spadesuit \, $ Banyak cara berpakaian menggunakan aturan perkalian :
Total = 3.4.3=36 cara.
Jadi, total berpakaian ada 36 cara. $\heartsuit $
$\spadesuit \, $ Ada 3S, 4B, dan 3C
$\spadesuit \, $ Banyak cara berpakaian menggunakan aturan perkalian :
Total = 3.4.3=36 cara.
Jadi, total berpakaian ada 36 cara. $\heartsuit $
Nomor 39
Sebuah kotak berisi 6 bola merah dan 4 bola putih. Dari dalam kotak diambil 3 bola sekaligus, banyak cara pengambilan sedemikian
hingga sedikitnya terdapat 2 bola putih adalah ...
$\clubsuit \, $ Misalkan : M = bola merah, P = bola putih
$\clubsuit \, $ Ada 6M dan 4P, diambil 3 bola sekaligus dengan sedikitnya 2 bola putih.
Ada beberapa kemungkinan :
1. 2P1M (2 putih dan 1 merah) ada $C_2^4.C_1^6=6.6=36 \, $ cara.
2. 3P0M (3 putih dan 0 merah) ada $C_3^4.C_0^6=4.1=4 \, $ cara.
keterangan : simbol $C$ artinya kombinasi.
Jadi, totalnya ada 40 cara pengambilan.$\heartsuit$
$\clubsuit \, $ Ada 6M dan 4P, diambil 3 bola sekaligus dengan sedikitnya 2 bola putih.
Ada beberapa kemungkinan :
1. 2P1M (2 putih dan 1 merah) ada $C_2^4.C_1^6=6.6=36 \, $ cara.
2. 3P0M (3 putih dan 0 merah) ada $C_3^4.C_0^6=4.1=4 \, $ cara.
keterangan : simbol $C$ artinya kombinasi.
Jadi, totalnya ada 40 cara pengambilan.$\heartsuit$
Nomor 40
Sebuah kotak berisi 6 bola merah dan 4 bola kuning. Dari kotak tersebut diambil tiga bola sekaligus. Peluang bahwa bola yang terambil
dua bola merah dan satu bola kuning sama dengan ...
$\spadesuit \, $ Misalkan : M = bola merah, K = bola kuning
$\spadesuit \, $ Ada 6M dan 4K, diambil 3 bola sekaligus : $n(S)=C_3^{10}=120$
$\spadesuit \, $ Harapannya terambil 2M1K : $n(A)=C_2^6.C_1^4=15\times 4 = 60$
$\spadesuit \, $ Peluangnya : $P(A)=\frac{n(A)}{n(S)}=\frac{1}{2}$
Jadi, peluang terambilnya 2M dan 1K adalah $\frac{1}{2} . \heartsuit $
$\spadesuit \, $ Ada 6M dan 4K, diambil 3 bola sekaligus : $n(S)=C_3^{10}=120$
$\spadesuit \, $ Harapannya terambil 2M1K : $n(A)=C_2^6.C_1^4=15\times 4 = 60$
$\spadesuit \, $ Peluangnya : $P(A)=\frac{n(A)}{n(S)}=\frac{1}{2}$
Jadi, peluang terambilnya 2M dan 1K adalah $\frac{1}{2} . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.