Nomor 11
Diketahui fungsi $f:R \rightarrow R$ dan $g:R \rightarrow R$ yang dinyatakan $f(x)=2x-1$ dan $g(x)=\frac{x}{x+2} , x\neq -2$. Invers $(fog)(x)$ adalah ...
$\spadesuit \, $ Invers : $y=\frac{ax+b}{cx+d} \Rightarrow y^{-1}=\frac{dx-b}{-cx+a} $
$\spadesuit \, $ Menentukan $(fog)(x)$ dan $(fog)^{-1}(x)$ :
$\begin{align*} (fog)(x) &= f(g(x)) \\ &= f \left( \frac{x}{x+2} \right) \\ &= 2.\left( \frac{x}{x+2} \right) -1 \\ &= \frac{2x-(x+2)}{x+2} \\ &= \frac{x-2}{x+2} \\ (fog)^{-1}(x) &= \frac{2x+2}{-x+1} = \frac{2x+2}{1-x} , \, \, \, x \neq 1 \end{align*}$
Jadi, Invers $(fog)(x)$ adalah $ (fog)^{-1}(x)=\frac{2x+2}{1-x} . \heartsuit $
$\spadesuit \, $ Menentukan $(fog)(x)$ dan $(fog)^{-1}(x)$ :
$\begin{align*} (fog)(x) &= f(g(x)) \\ &= f \left( \frac{x}{x+2} \right) \\ &= 2.\left( \frac{x}{x+2} \right) -1 \\ &= \frac{2x-(x+2)}{x+2} \\ &= \frac{x-2}{x+2} \\ (fog)^{-1}(x) &= \frac{2x+2}{-x+1} = \frac{2x+2}{1-x} , \, \, \, x \neq 1 \end{align*}$
Jadi, Invers $(fog)(x)$ adalah $ (fog)^{-1}(x)=\frac{2x+2}{1-x} . \heartsuit $
Nomor 12
Di Zedland ada dua media massa koran yang sedang mencari orang untuk bekerja sebagai penjual koran. Iklan di bawah ini menunjukkan bagaimana
mereka membayar gaji penjual koran.

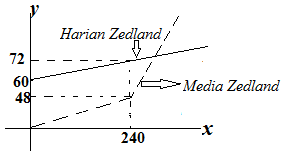
Joko memutuskan untuk melamar menjadi penjual koran. Ia perlu memilih bekerja pada Media Zedland atau Harian Zedland . Grafik manakah di bawah ini yang menggambarkan bagaimana koran membayar penjual-penjualnya?

Joko memutuskan untuk melamar menjadi penjual koran. Ia perlu memilih bekerja pada Media Zedland atau Harian Zedland . Grafik manakah di bawah ini yang menggambarkan bagaimana koran membayar penjual-penjualnya?
$\clubsuit \, $ Misalkan, banyak koran adalah $x$ :
$\clubsuit \, $ Koran Harian Zedland
0,05 per koran ($0,05x$) dan mendapatkan 60 zed, sehingga totalnya : $0,05x+60$
persamaannya : $y=0,05x+60$
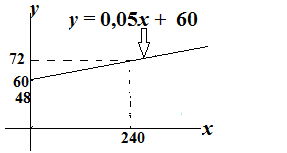
$\clubsuit \, $ Koran Media Zedland
Sebelum 240 koran, gaji = $0,20x$ dan selebihnya 0,40 sehingga perkoran menjadi 0,60, gaji = $0,60x$
persamaannya : $y=0,20x$ untuk $x\leq 240$ dan $y=0,60x$ untuk $x>240$
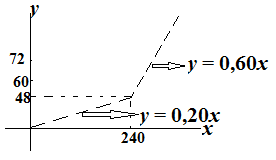
Jadi, gabungan kedua gambar: $\heartsuit $
$\clubsuit \, $ Koran Harian Zedland
0,05 per koran ($0,05x$) dan mendapatkan 60 zed, sehingga totalnya : $0,05x+60$
persamaannya : $y=0,05x+60$
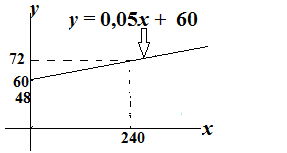
$\clubsuit \, $ Koran Media Zedland
Sebelum 240 koran, gaji = $0,20x$ dan selebihnya 0,40 sehingga perkoran menjadi 0,60, gaji = $0,60x$
persamaannya : $y=0,20x$ untuk $x\leq 240$ dan $y=0,60x$ untuk $x>240$
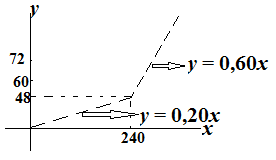
Jadi, gabungan kedua gambar: $\heartsuit $

Nomor 13
Diketahui matriks $A= \left( \begin{matrix}2x & 3 \\ -3 & -1 \end{matrix} \right) , B= \left( \begin{matrix} x-y & y+1 \\ 0 & 3 \end{matrix} \right) , \text{dan} C= \left( \begin{matrix} -4 & -3 \\ 5 & 2 \end{matrix} \right) $ .
Jika $C^t$ adalah transpose dari matriks $C$ dan $A+B=C^t$, nilai dari $2x+3y=...$
$\begin{align*}
A+B &= A^t \\
\left( \begin{matrix}2x & 3 \\ -3 & -1 \end{matrix} \right) + \left( \begin{matrix} x-y & y+1 \\ 0 & 3 \end{matrix} \right) &= \left( \begin{matrix} -4 & 5 \\ -3 & 2 \end{matrix} \right) \\
\left( \begin{matrix} 3x-y & y+4 \\ -3 & 2 \end{matrix} \right) &= \left( \begin{matrix} -4 & 5 \\ -3 & 2 \end{matrix} \right) \\
y+4 = 5 \Rightarrow & y=1 \\
3x-y = -4 \Rightarrow & 3x -1 =-4 \Rightarrow x=-1
\end{align*} $
sehingga $2x+3y=2.(-1)+3.1=1$
Jadi, nilai $2x+3y=1 . \heartsuit $
sehingga $2x+3y=2.(-1)+3.1=1$
Jadi, nilai $2x+3y=1 . \heartsuit $
Nomor 14
Diketahui vektor-vektor $\vec{a}=\left( \begin{matrix} 1 \\ 2 \\ -3 \end{matrix} \right), \vec{b}=\left( \begin{matrix} 4 \\ 4 \\ m \end{matrix} \right), \text{dan} \vec{c}=\left( \begin{matrix} 3 \\ -4 \\ 5 \end{matrix} \right)$.
Jika $\vec{a}$ tegak lurus $\vec{b}$, hasil dari $\vec{a}+\vec{b}-2\vec{c} = ...$
$\spadesuit \, $ Hubungan tegak lurus , $\vec{a} \bot \vec{b} \Rightarrow \vec{a}.\vec{b}=0$ , sehingga diperoleh :
$\begin{align*} \vec{a}.\vec{b}&=0 \\ \left( \begin{matrix} 1 \\ 2 \\ -3 \end{matrix} \right).\left( \begin{matrix} 4 \\ 4 \\ m \end{matrix} \right) &= 0 \\ 4+8-3m &= 0 \Rightarrow m=4 \\ \text{sehingga vektor } \, \vec{b} = \left( \begin{matrix} 4 \\ 4 \\ 4 \end{matrix} \right) \end{align*} $
$\vec{a}+\vec{b}-2\vec{c}=\left( \begin{matrix} 1 \\ 2 \\ -3 \end{matrix} \right) + \left( \begin{matrix} 4 \\ 4 \\ 4 \end{matrix} \right) - \left( \begin{matrix} 6 \\ -8 \\ 10 \end{matrix} \right) = \left( \begin{matrix} -1 \\ 14 \\ -9 \end{matrix} \right) $
Jadi, nilai $\vec{a}+\vec{b}-2\vec{c} = \left( \begin{matrix} -1 \\ 14 \\ -9 \end{matrix} \right) . \, \heartsuit $
$\begin{align*} \vec{a}.\vec{b}&=0 \\ \left( \begin{matrix} 1 \\ 2 \\ -3 \end{matrix} \right).\left( \begin{matrix} 4 \\ 4 \\ m \end{matrix} \right) &= 0 \\ 4+8-3m &= 0 \Rightarrow m=4 \\ \text{sehingga vektor } \, \vec{b} = \left( \begin{matrix} 4 \\ 4 \\ 4 \end{matrix} \right) \end{align*} $
$\vec{a}+\vec{b}-2\vec{c}=\left( \begin{matrix} 1 \\ 2 \\ -3 \end{matrix} \right) + \left( \begin{matrix} 4 \\ 4 \\ 4 \end{matrix} \right) - \left( \begin{matrix} 6 \\ -8 \\ 10 \end{matrix} \right) = \left( \begin{matrix} -1 \\ 14 \\ -9 \end{matrix} \right) $
Jadi, nilai $\vec{a}+\vec{b}-2\vec{c} = \left( \begin{matrix} -1 \\ 14 \\ -9 \end{matrix} \right) . \, \heartsuit $
Nomor 15
Diketahui vektor-vektor $\vec{u}=b\vec{i}+a\vec{j}+9\vec{k}$ dan $\vec{v}=a\vec{i}+-b\vec{j}+a\vec{k}$. Sudut antara vektor $\vec{u}$ dan $\vec{v}$
adalah $\theta$ dengan $cos\theta = \frac{6}{11}$. Proyeksi $\vec{u}$ pada $\vec{v}$ adalah $\vec{p}=4\vec{i}+-2\vec{j}+4\vec{k}$. Nilai dari $b=...$
$\clubsuit \, $ Perkalian dot : $\vec{u}.\vec{v} =ab-ab+9a=9a \, \, $ dan $\, \, \vec{u}.\vec{v} = |\vec{u}| |\vec{v}| cos \theta $
$\begin{align*} \vec{u}.\vec{v} &= |\vec{u}| |\vec{v}| cos \theta \\ 9a &= \left( \sqrt{a^2+b^2+9^2} \sqrt{a^2+b^2+a^2} \right) . \frac{6}{11} \, \, \, \text{...pers(i)} \end{align*} $
$\clubsuit \, $ Proyeksi vektor $\vec{u}$ pada $\vec{v}$ adalah $\vec{p}$ :
$\begin{align*} \vec{p} &= \left( \frac{\vec{u}.\vec{v}}{|\vec{v}|^2} \right) \vec{v} \\ \left( \begin{matrix} 4 \\ -2 \\ 4 \end{matrix} \right) &= \frac{9a}{\left( \sqrt{a^2+b^2+a^2} \right)^2} \left( \begin{matrix} a \\ -b \\ a \end{matrix} \right) \end{align*} $
Persamaan yang terbentuk :
$4 = \frac{9a}{\left( \sqrt{a^2+b^2+a^2} \right)^2} . a \, \, \, \text{...pers(ii)} $
$-2 = \frac{9a}{\left( \sqrt{a^2+b^2+a^2} \right)^2} . (-b) \, \, \, \text{...pers(iii)} $
$\clubsuit \, $ Bagi pers(ii) dan pers(iii) , diperoleh :
$-2=\frac{-a}{b} \Rightarrow a=2b $
$\clubsuit \, $ Substitusi $a=2b$ ke pers(i) :
$\begin{align*} 9a &= \left( \sqrt{a^2+b^2+9^2} \sqrt{a^2+b^2+a^2} \right) . \frac{6}{11} \, \, \, \text{...pers(i)} \\ 9.2b &= \left( \sqrt{(2b)^2+b^2+81} \sqrt{(2b)^2+b^2+(2b)^2} \right) . \frac{6}{11} \\ \not{18}b &= \left( \sqrt{4b^2+b^2+81} \sqrt{4b^2+b^2+4b^2} \right) . \frac{\not{6}}{11} \\ 3b &= \left( \sqrt{5b^2+81} \sqrt{9b^2} \right) . \frac{1}{11} \\ 11. \not{3b} &= \left( \sqrt{5b^2+81} \right) . \not{3b} \\ \sqrt{5b^2+81} &= 11 \, \, \text{(kuadratkan)} \\ 5b^2+81 &= 121 \\ b^2 &= 8 \\ b &= \pm 2\sqrt{2} \end{align*} $
Jadi, nilai $b=2\sqrt{2} . \heartsuit $
$\begin{align*} \vec{u}.\vec{v} &= |\vec{u}| |\vec{v}| cos \theta \\ 9a &= \left( \sqrt{a^2+b^2+9^2} \sqrt{a^2+b^2+a^2} \right) . \frac{6}{11} \, \, \, \text{...pers(i)} \end{align*} $
$\clubsuit \, $ Proyeksi vektor $\vec{u}$ pada $\vec{v}$ adalah $\vec{p}$ :
$\begin{align*} \vec{p} &= \left( \frac{\vec{u}.\vec{v}}{|\vec{v}|^2} \right) \vec{v} \\ \left( \begin{matrix} 4 \\ -2 \\ 4 \end{matrix} \right) &= \frac{9a}{\left( \sqrt{a^2+b^2+a^2} \right)^2} \left( \begin{matrix} a \\ -b \\ a \end{matrix} \right) \end{align*} $
Persamaan yang terbentuk :
$4 = \frac{9a}{\left( \sqrt{a^2+b^2+a^2} \right)^2} . a \, \, \, \text{...pers(ii)} $
$-2 = \frac{9a}{\left( \sqrt{a^2+b^2+a^2} \right)^2} . (-b) \, \, \, \text{...pers(iii)} $
$\clubsuit \, $ Bagi pers(ii) dan pers(iii) , diperoleh :
$-2=\frac{-a}{b} \Rightarrow a=2b $
$\clubsuit \, $ Substitusi $a=2b$ ke pers(i) :
$\begin{align*} 9a &= \left( \sqrt{a^2+b^2+9^2} \sqrt{a^2+b^2+a^2} \right) . \frac{6}{11} \, \, \, \text{...pers(i)} \\ 9.2b &= \left( \sqrt{(2b)^2+b^2+81} \sqrt{(2b)^2+b^2+(2b)^2} \right) . \frac{6}{11} \\ \not{18}b &= \left( \sqrt{4b^2+b^2+81} \sqrt{4b^2+b^2+4b^2} \right) . \frac{\not{6}}{11} \\ 3b &= \left( \sqrt{5b^2+81} \sqrt{9b^2} \right) . \frac{1}{11} \\ 11. \not{3b} &= \left( \sqrt{5b^2+81} \right) . \not{3b} \\ \sqrt{5b^2+81} &= 11 \, \, \text{(kuadratkan)} \\ 5b^2+81 &= 121 \\ b^2 &= 8 \\ b &= \pm 2\sqrt{2} \end{align*} $
Jadi, nilai $b=2\sqrt{2} . \heartsuit $
Cara II :
$\clubsuit \, $ Perkalian dot : $\vec{u}.\vec{v} =ab-ab+9a=9a \, \, $ dan $\, \, \vec{u}.\vec{v} = |\vec{u}| |\vec{v}| cos \theta $
$\begin{align*} \vec{u}.\vec{v} &= |\vec{u}| |\vec{v}| cos \theta \\ 9a &= \left( \sqrt{a^2+b^2+9^2} \sqrt{a^2+b^2+a^2} \right) . \frac{6}{11} \, \, \, \text{...pers(i)} \end{align*} $
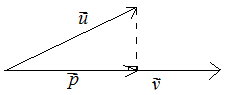
$\clubsuit \, $ Hasil proyeksi $\vec{u}$ pada $\vec{v}$ adalah $\vec{p}$ yang artinya $\vec{p}$ sejajar dengan $\vec{v}$ , sehingga
$\begin{align*} \vec{p} &= n.\vec{v} \\ \left( \begin{matrix} 4 \\ -2 \\ 4 \end{matrix} \right) &= n \left( \begin{matrix} a \\ -b \\ a \end{matrix} \right) \\ \left( \begin{matrix} 4 \\ -2 \\ 4 \end{matrix} \right) &= \left( \begin{matrix} an \\ -bn \\ an \end{matrix} \right) \end{align*} $
Diperoleh :
$4 = an \Rightarrow n=\frac{4}{a}$
$-2 = -bn \Rightarrow -2 = -b. \frac{4}{a} \Rightarrow a= 2b $
$\clubsuit \, $ Substitusi $a=2b$ ke pers(i) :
$\begin{align*} 9a &= \left( \sqrt{a^2+b^2+9^2} \sqrt{a^2+b^2+a^2} \right) . \frac{6}{11} \, \, \, \text{...pers(i)} \\ 9.2b &= \left( \sqrt{(2b)^2+b^2+81} \sqrt{(2b)^2+b^2+(2b)^2} \right) . \frac{6}{11} \\ \not{18}b &= \left( \sqrt{4b^2+b^2+81} \sqrt{4b^2+b^2+4b^2} \right) . \frac{\not{6}}{11} \\ 3b &= \left( \sqrt{5b^2+81} \sqrt{9b^2} \right) . \frac{1}{11} \\ 11. \not{3b} &= \left( \sqrt{5b^2+81} \right) . \not{3b} \\ \sqrt{5b^2+81} &= 11 \, \, \text{(kuadratkan)} \\ 5b^2+81 &= 121 \\ b^2 &= 8 \\ b &= \pm 2\sqrt{2} \end{align*} $
Jadi, nilai $b=2\sqrt{2} . \heartsuit $
$\clubsuit \, $ Perkalian dot : $\vec{u}.\vec{v} =ab-ab+9a=9a \, \, $ dan $\, \, \vec{u}.\vec{v} = |\vec{u}| |\vec{v}| cos \theta $
$\begin{align*} \vec{u}.\vec{v} &= |\vec{u}| |\vec{v}| cos \theta \\ 9a &= \left( \sqrt{a^2+b^2+9^2} \sqrt{a^2+b^2+a^2} \right) . \frac{6}{11} \, \, \, \text{...pers(i)} \end{align*} $
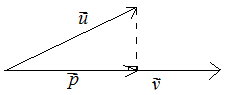
$\clubsuit \, $ Hasil proyeksi $\vec{u}$ pada $\vec{v}$ adalah $\vec{p}$ yang artinya $\vec{p}$ sejajar dengan $\vec{v}$ , sehingga
$\begin{align*} \vec{p} &= n.\vec{v} \\ \left( \begin{matrix} 4 \\ -2 \\ 4 \end{matrix} \right) &= n \left( \begin{matrix} a \\ -b \\ a \end{matrix} \right) \\ \left( \begin{matrix} 4 \\ -2 \\ 4 \end{matrix} \right) &= \left( \begin{matrix} an \\ -bn \\ an \end{matrix} \right) \end{align*} $
Diperoleh :
$4 = an \Rightarrow n=\frac{4}{a}$
$-2 = -bn \Rightarrow -2 = -b. \frac{4}{a} \Rightarrow a= 2b $
$\clubsuit \, $ Substitusi $a=2b$ ke pers(i) :
$\begin{align*} 9a &= \left( \sqrt{a^2+b^2+9^2} \sqrt{a^2+b^2+a^2} \right) . \frac{6}{11} \, \, \, \text{...pers(i)} \\ 9.2b &= \left( \sqrt{(2b)^2+b^2+81} \sqrt{(2b)^2+b^2+(2b)^2} \right) . \frac{6}{11} \\ \not{18}b &= \left( \sqrt{4b^2+b^2+81} \sqrt{4b^2+b^2+4b^2} \right) . \frac{\not{6}}{11} \\ 3b &= \left( \sqrt{5b^2+81} \sqrt{9b^2} \right) . \frac{1}{11} \\ 11. \not{3b} &= \left( \sqrt{5b^2+81} \right) . \not{3b} \\ \sqrt{5b^2+81} &= 11 \, \, \text{(kuadratkan)} \\ 5b^2+81 &= 121 \\ b^2 &= 8 \\ b &= \pm 2\sqrt{2} \end{align*} $
Jadi, nilai $b=2\sqrt{2} . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.